How do you use synthetic division to find factors for #x^3 + 2x^2 - 5x - 6#?
1 Answer
Noting that
Complete factors:
Explanation:
Part 1: The initial Factor
If
then setting the negative terms on one side and the positive terms on the other:
then testing a few values:
#{: (x,color(white)("XX"),x^3+2x^2,color(white)("XX"),5x+6), (0,color(white)("XX"),0,color(white)("XX"),6), (1,color(white)("XX"),3,color(white)("XX"),11), (2,color(white)("XX"),16,color(white)("XX"),16) :}#
So if#x=2# then#x^3+2x^2-5x-6 =0#
#rarr (x-2)# is a factor of#x^3+2x^2-5x-6#
Part 2: Use of synthetic division
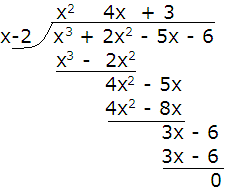
So
Part 3: Factoring the remaining quadratic
By observation or using the quadratic formula we can factor:
Part 4: Summarize results
