How do you use synthetic division to find the factors of #f(x)= x^4 -x^3 -19x^2+49x-30#?
1 Answer
Aug 30, 2015
If you can spot a factor of
Hence we can find:
Explanation:
First note that
Use synthetic division to divide

So
Notice that
Divide
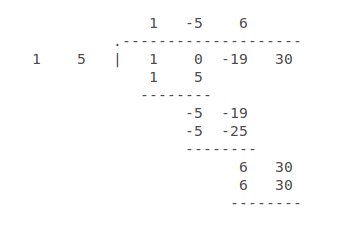
So
By this stage you can probably spot that

