How do you use synthetic division to find the zeroes of #f(x)= x^4 -3x^3-9x^2-3x-10#?
1 Answer
The zeroes of
Explanation:
According to the rational root theorem, the rational roots of
So the only possible rational roots are
We have to test all eight possibilities.
Here are the only two that work.
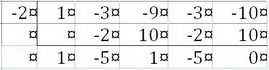
and

So
That means that
We can use synthetic division to find the other factor.
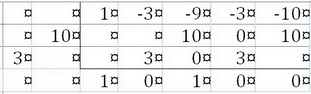
The other factor is
So
and
The roots of

