How do you use synthetic division to see if -1 is a zero of #h(x)=x^4+9x^3+18x-8#?

Question

1360 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-07-23T23:26:20

#-1# is not a zero of #h(x) = x^4 +9x^3+18x-8#

Step 1. Write only the coefficients of #x# inside an upside-down division symbol.

Step 2. Put the test zero, #x= -1#, at the left.

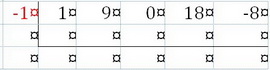
Step 3. Drop the first coefficient below the division symbol.

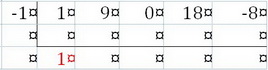
Step 4. Multiply the drop-down by the test zero, and put the result in the next column.

Step 5. Add down the column.

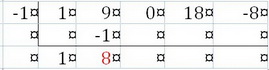
Step 6. Repeat Steps 4 and 5 until you can go no farther.

#-1# is not a zero of #h(x)# because the division gives a remainder of #-34#.

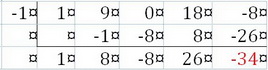
Check:

#(x+1)(x^3+8x^2-8x+26 -34/(x+1))#

#= (x+1)(x^3+8x^2-8x+26) -34#

#= x^4+8x^3-cancel(8x^2)+26x+x^3+cancel(8x^2)-8x+26 -34#

#= x^4+9x^3+18x-8#