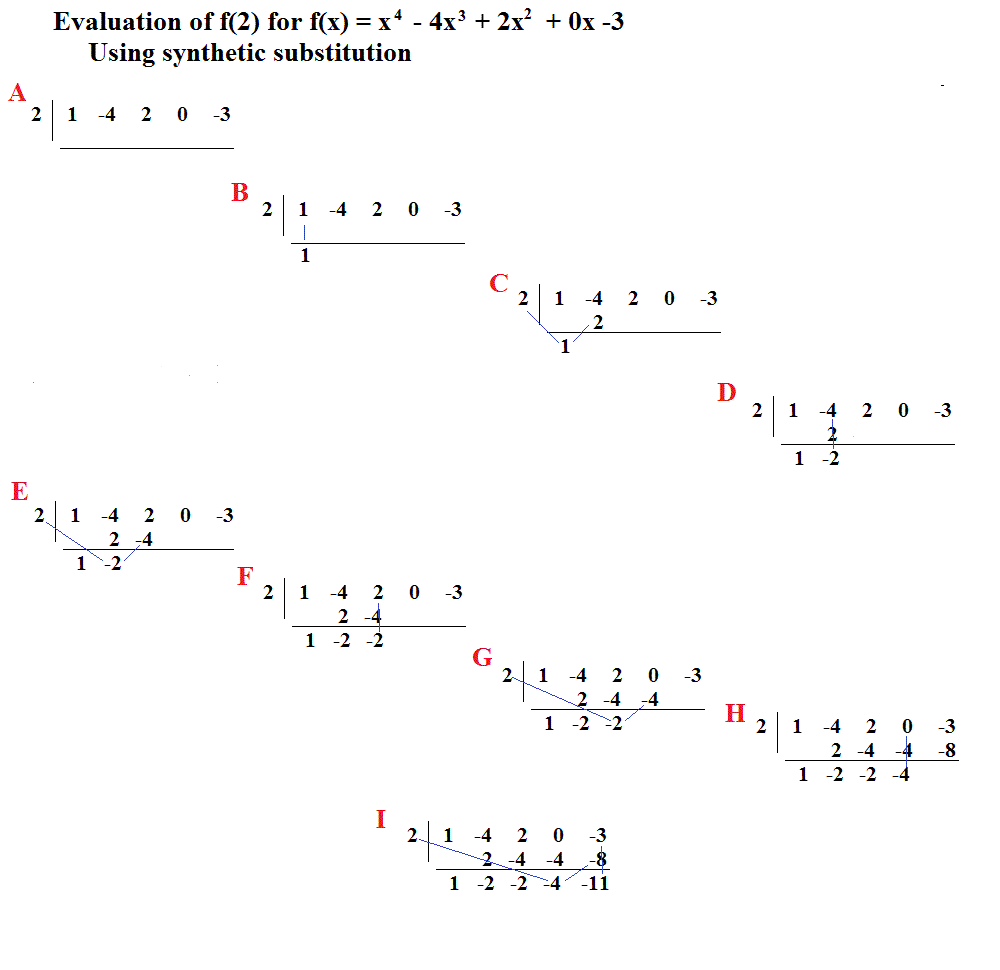
Rewrite #f(x)# so all powers of #x# are represented (in descending power sequence).
#color(white)("XXXX")##f(x)=x^4-4x^3+2x^2+0x-3#
#color(red)("[A]")##color(white)("XXXX")#Write the substitution value (#2#) separated by a vertical bar from a row of the from the coefficients as noted above.
#color(white)("XXXXXX")#Draw a vertical line below the coefficients, allowing enough space to write another row of numbers between the coefficients and the line.
#color(red)("[B]")##color(white)("XXXX")#Copy the first coefficient to a position below the line.
#color(red)("[C]")##color(white)("XXXX")#Multiply the substitution value and the number just written below the line and record the product above the line under the second coefficient.
#color(red)("[D]")##color(white)("XXXX")#Add the product just developed and the second coefficient and write the sum below the line.
#color(red)("[E]")##color(white)("XXXX")#Multiply the substitution value and the number just written below the line and record the product below the line.
#color(red)("[F] to [I]")##color(white)("XXXX")#Continue this process until all coefficients have been processed.
#color(red)("[I]")#The solution is the last value written below the line.