Question

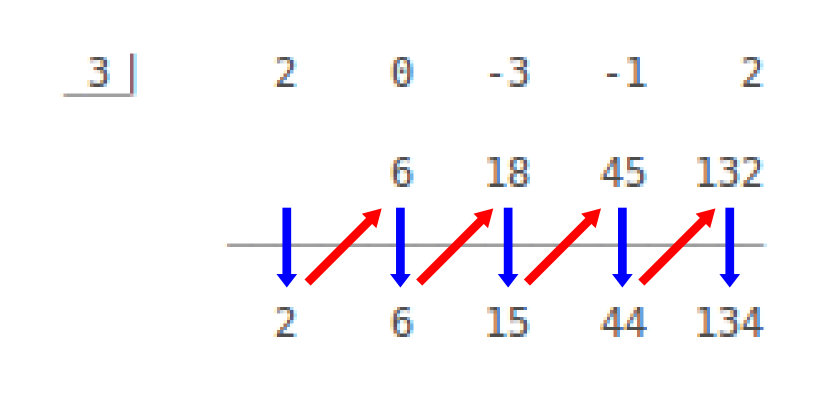
How do you use synthetic substitution to find f(3) for `f(x) = 2x^4 - 3x^2 - x + 2`?

Answer 1

If `f(x)=2x^4−3x^2−x+2`
then `f(3) = 134`
`color(white)("XXXX")`(evaluated using synthetic substitution)#

Explanation:

Rewrite the given expression to include all powers of `x` (in descending sequence)
`f(x) = 2x^4 +0x^3-3x^2-1x+2`

Write the argument value (in this case the `3` from `f(3)`) to the left and then on the same line the coefficients of `x` (from above).

[1]
Copy the coefficient of the highest order term on the next line under its coefficient.
Multiply the value just copied by the argument and write the product under the coefficient of the next lower term.
(see chart below for full progression).

[2]
Add the product calculated on the previous step to the original coefficient value above it and write the sum beneath these numbers.
Multiply the sum you just calculated by the argument and write the product under the coefficient of the next lower term.

[3] to [5]
Repeat the actions described in [2]

#{: (3xx, , 2, , 0, , -3, , -1, , 2), ( , , , , , , , , , , ), ( "[1]" ,rarr, 2,"=", 6, , , , , , ), ( "[2]" ,rarr, rarr ,rarr, 6,"=", 18, , , , ), ( "[3]" ,rarr, rarr,rarr, rarr,rarr , 15,"=", 45, , ), ( "[4]" ,rarr, rarr,rarr,rarr ,rarr,rarr ,rarr , 44,"=",132), ( "[5]" ,rarr ,rarr ,rarr, rarr,rarr, rarr,rarr,rarr,rarr,134) :}#

The final sum is the solution to the equation for the given argument value.

Here's a picture. The blue arrows represent addition, the red arrows multiplication by the argument `3`...