How do you use the disk or shell method to find the volume of the solid generated by revolving the regions bounded by the graphs of #y = x^(1/2)#, #y = 2#, and #x = 0# about the line #x = -1#?
1 Answer
See the explanation section, below.
Explanation:
Here is a picture of the region with a thin slice taken vertically.
So thickness is
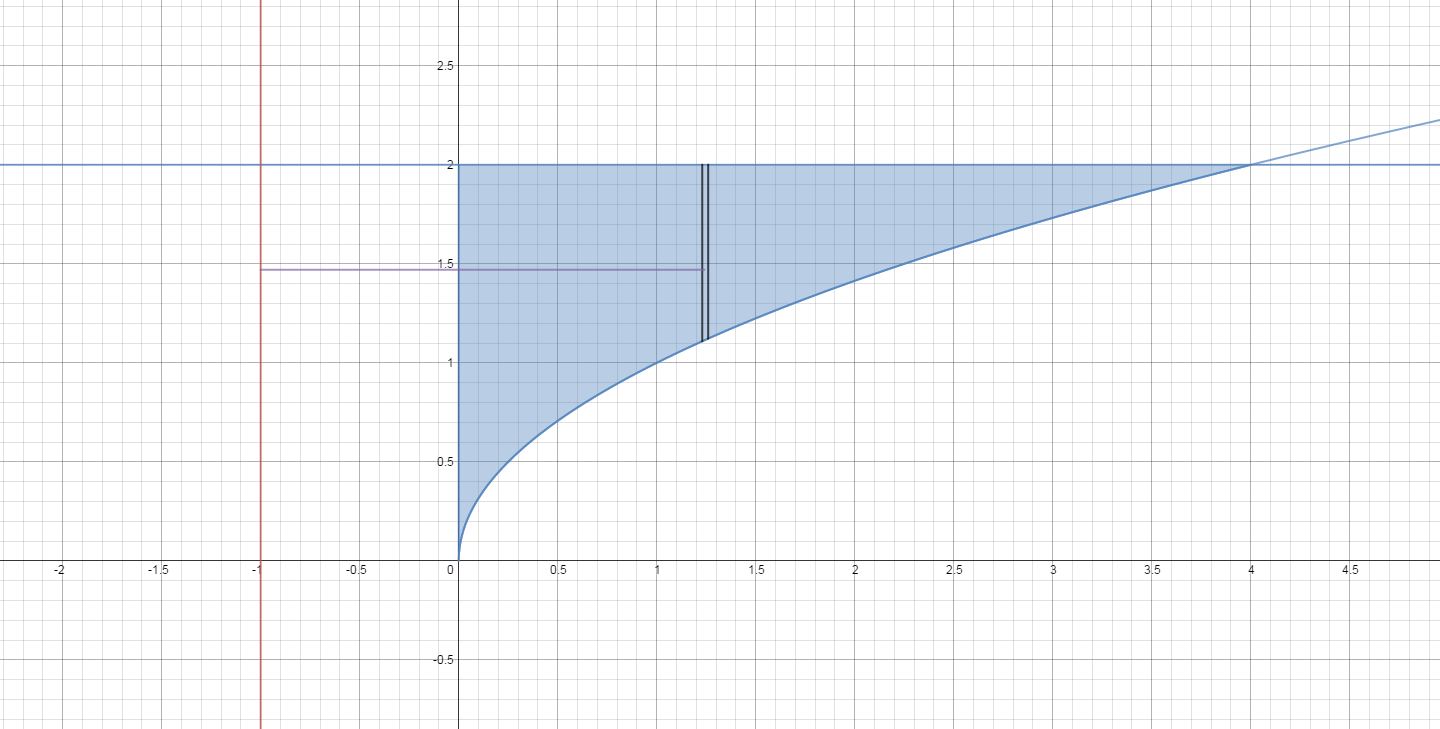
The representative shell will have volume
We see that the values of
So the volume of the solid is found by evaluating:
Expand the product and integrate term by term.
To use disks/washers , we need to take our slices perpendicular to the axis of rotation as shown below.
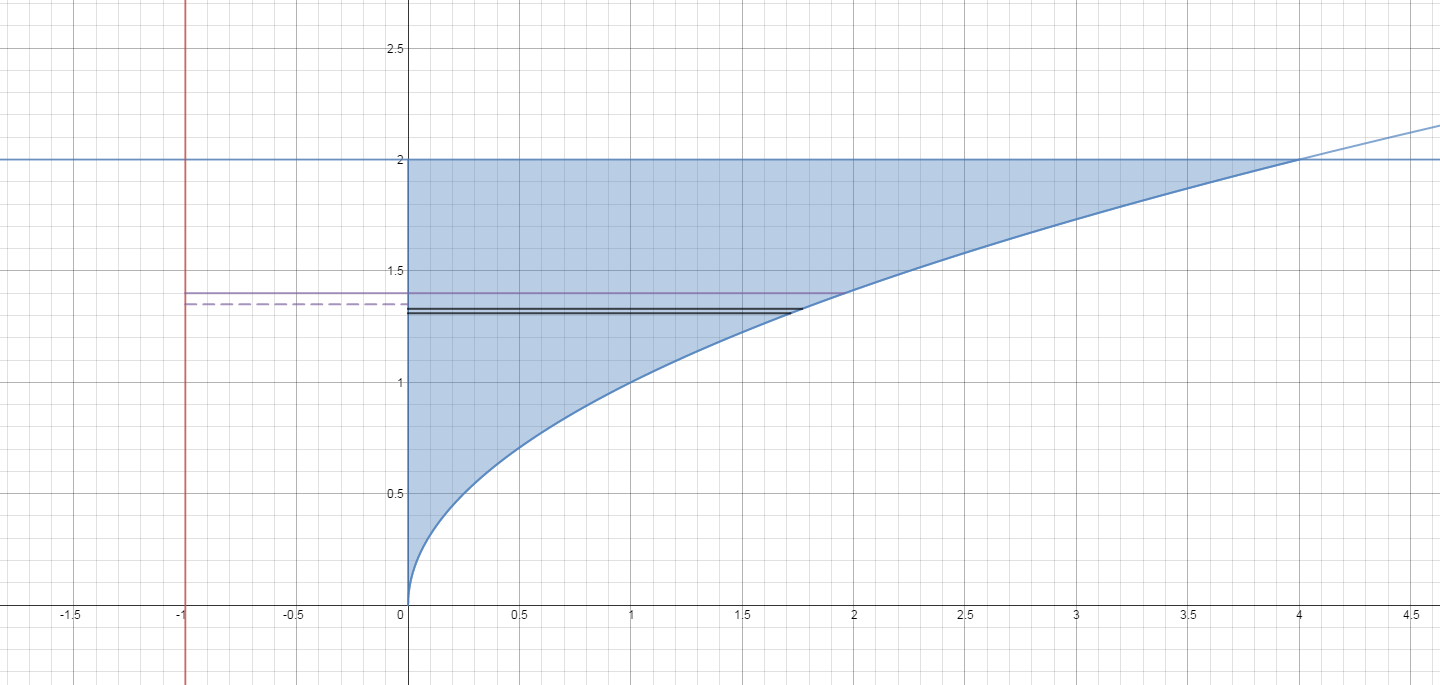
The curve is now expressed as
The representative washer has volume:
Again, expand and integrate term by term.

