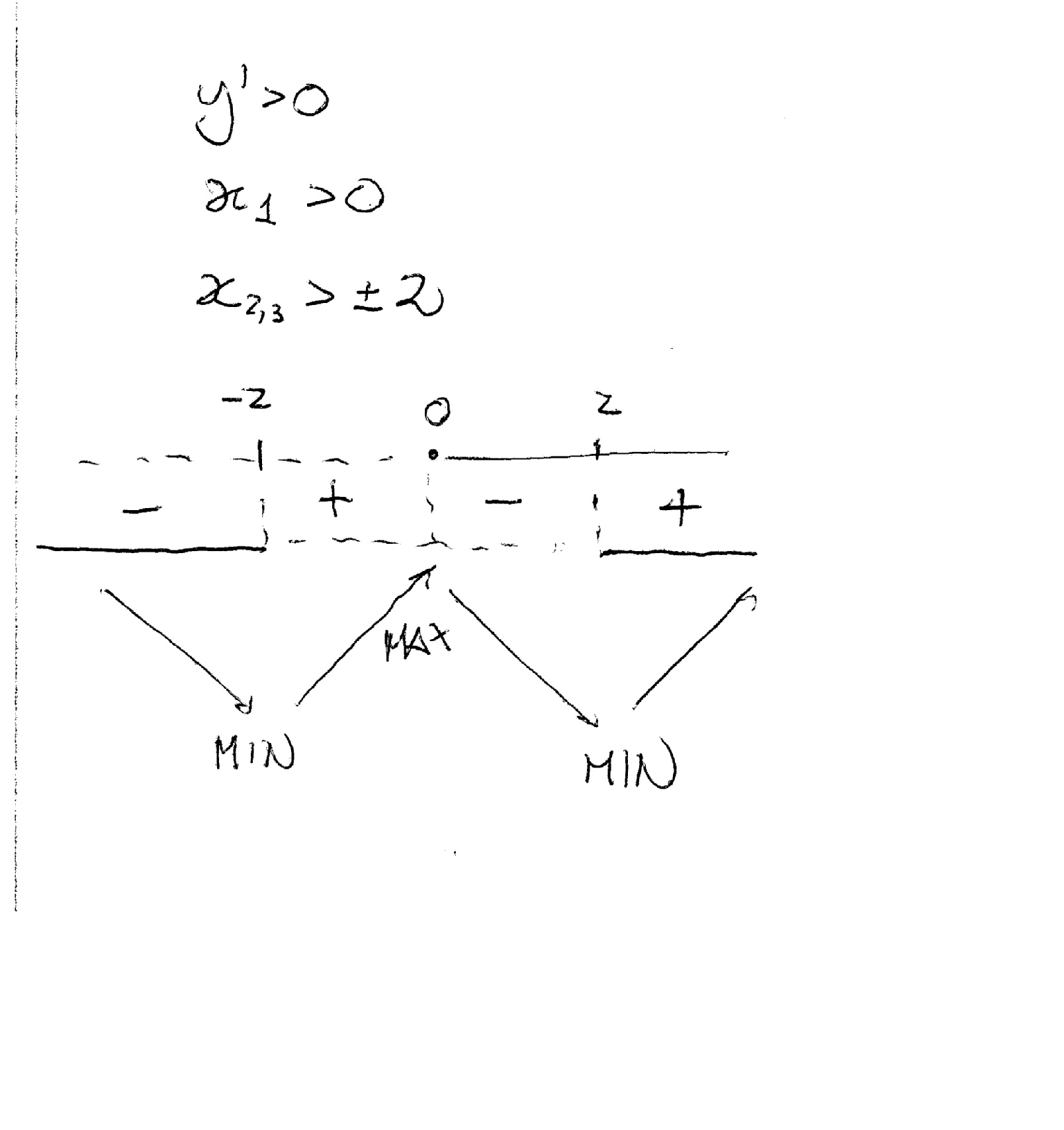
How do you use the first derivative test to determine whether the critical point is a local maximum, local minimum, or neither for #y=x^4 - 8x^2#?
1 Answer
Mar 28, 2015
First evaluate the first derivative:
Second, set it equal to zero;
you get:
and so:
This gives you the critical points (where the inclination of your curve changes).
Third set your derivative >0, and study the combined signs of the derivatives: