How do you use the fundamental theorem of calculus and what can it be used for?
1 Answer
The main application is to find exact answers for various kinds of definite integrals. Another application is that it allows us to construct antiderivatives (in a theoretical way).
Explanation:
Here's a simple example where the Fundamental Theorem of Calculus allows us to find the value of a definite integral. Let
An example of how the Fundamental Theorem of Calculus can be used to construct an antiderivative. Let
However, if we let the upper limit of integration of
What good is this function? Evidently it is important enough in applications to be given a name. It's a "Fresnel function " and it has applications to optics and highway design.
Can it be approximated and graphed? Yes. Use numerical integration approximation techniques like Simpson's Rule to find values of
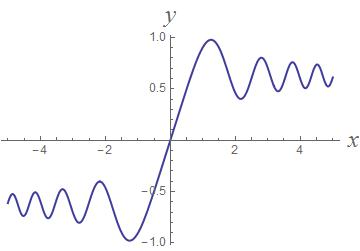
As an exercise, see if you can find the critical points and approximate local extreme values of this function.

