Question

How do you use the half angle identity to find sin 105?

Answer 1

`sin105^@=sqrt(2+sqrt3)/2`

Explanation:

We need to use the half angle formula:

`sin(theta/2)=+-sqrt((1-costheta)/2)`

In this case, we want to find `sin(105^@)`, so that's what we want `sin(theta/2)` to equal. To find out what our `theta` is, set these to equal to each other:

`sin(105^@)=sin(theta/2)`

`105^@=theta/2`

`210^@=theta`

This is our `theta`. Now, we can use the half angle formula:

`color(white)=sin(105^@)`

`=sin(210^@/2)`

`=+-sqrt((1-cos(210^@))/2)`

`=+-sqrt((1-(-sqrt3/2))/2)`

`=+-sqrt((1+sqrt3/2)/2)`

`=+-sqrt((1+sqrt3/2)/2)`

`=+-sqrt((2+sqrt3)/4)`

`=+-sqrt(2+sqrt3)/sqrt4`

`=+-sqrt(2+sqrt3)/2`

Since `105^@` is in quadrant II, we know that our answer will be positive that angle is above the `x`-axis (and we are taking the sine). Therefore:

`sin105^@=sqrt(2+sqrt3)/2`

We can check our answer using a calculator (be sure it is in degrees mode):

https://www.desmos.com/calculator

Answer 2

`color(blue)(sin (105) = = +-(1/2) sqrt(2 + sqrt3)`

Explanation:

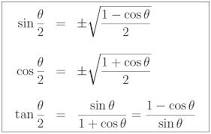http://www2.clarku.edu/~djoyce/trig/identities.html

Given `theta / 2 = 105^@ = (7pi)/12`

`theta = (7pi)/6`

`sin (theta/2) = +- sqrt((1 - cos theta)/2)`

`sin ((7pi)/12) = +- sqrt((1-cos (((7pi)/12)*2))/2)`

`sin ((7pi)/12) = +- sqrt((1 - cos ((7pi)/6))/2)`

But `cos ((7pi)/6) = cos (pi + pi/6) = - cos (pi/6)`

`:. sin ((7pi)/12) = +- sqrt((1 + cos(pi/6))/2)`

`=> +- sqrt((1 + sqrt(3)/2)/2)`

`=> +- sqrt((2 + sqrt3)/4) = +-(1/2) sqrt(2 + sqrt3)`