How do you use the Henderson-Hasselbalch to calculate the pH of a buffer solution that is .50 M in NH_3 and . 20 M in NH_4Cl?
For ammonia, pK_b=4.75 .
For ammonia,
1 Answer
That buffer solution has a pH of
Explanation:
Before I introduce Henderson-Hasselbalch's equation, we should identify the acid and base. Ammonia
Now, we can use this equation:
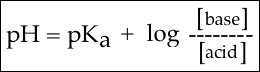 www.chemteam.info
www.chemteam.info
As you can see, we are given a pKb instead of a pKa. But, no worries we can use the following equation that relates both constants to each other:
We can solve for the pKa by subtracting the given pKb from 14:
Thus, your pKa is 9.25
Next, we can obtain the [base] and [acid] from the question.
[
We're not really concerned with the chloride anion that attached to the ammonium ion because it's a spectator ion and it has no effect on the buffer system.
Now, we have all of the information to determine the pH. Let's plug our values into the equation:

