Question

How do you use the integral test to determine whether the following series converge of diverge `sum n/((n^2+1)^2)` from n=1 to infinity? Thanks for the help !!! I have no idea on how to do these questions?

Answer 1

The series converges.

Explanation:

Let `f(x) = x/(x^2+1)^2`.

In order to use the intergral test, `f(x)` must be positive and decreasing on `[p;+oo[`.

Let's study the sign of `f(x)` :

`f(x)` is positive on `]0;+oo[`.

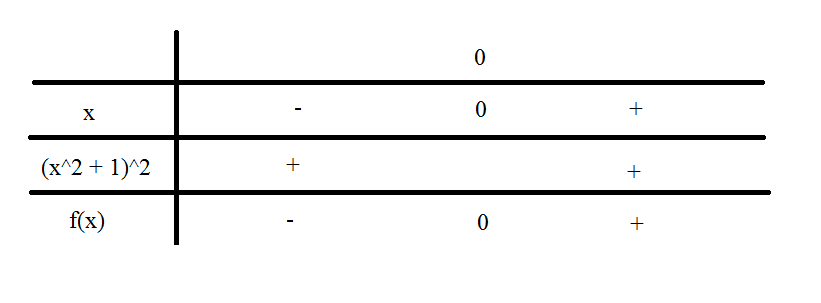
Let's study the slope of `f(x)` :

To find the derivative of `f(x)`, we will use the formula :

`((h(x))/(g(x)))' = (h'(x)g(x) - h(x)g'(x))/g^2(x)`

`f'(x) = ((x^2+1)^2-4x^2(x^2+1))/(x^2+1)^4 = (-3x^2+1)/(x^2+1)^3`

`f(x)` is decreasing on `]1/sqrt(3);+oo[`

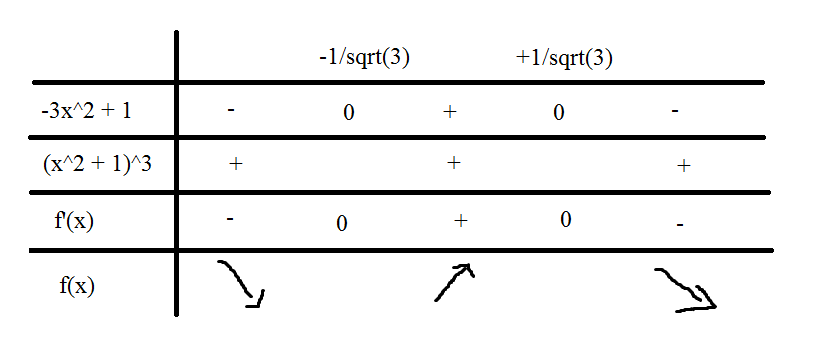
We want to use the integral test for n=1 to infinity. Since `f(x)` is positive and decreasing on `]1/sqrt(3);+oo[`, it is also true for `[1;+oo[`.

`f(x) = x/(x^2+1)^2 = x(x^2+1)^(-2)`

To find the integral of `f(x)`, we will use the formula :

`inth'(x)h^n(x)dx = 1/(n+1)h^(n+1)(x)`

`intf(x)dx = intx(x^2+1)^(-2)dx = 1/2int2x(x^2+1)^(-2)dx`

`= 1/2inth'(x)*h^(-2)(x)dx`, where `h(x) = (x^2+1)`

`=1/2 * (1/((-2)+1)h^(-2+1)(x)) = -1/2h^(-1)(x)`

`= -1/2(x^2+1)^-1 = -1/(2(x^2+1)) = F(x)`

The series converges if `int_(1)^(+oo)f(x)dx` exists.

`int_(1)^(+oo)f(x)dx = [F(x)]_(1)^(+oo) = ''F(+oo)'' - F(1)`

`= 0 - F(1) = -(-1/(1+1)^2) = +1/4`.

The series converges.

Answer 2

The integral test just says, basically:

By taking the integral of a positive, decreasing function `a_n` of some series `sum a_n` that works within the boundaries `[k, oo]`, if the integral is finite, the sum converges.

`n/(n^2 + 1)^2` is obviously decreasing since it's basically `n/n^4 = 1/n^3`, which decreases as `n->oo`. It's also certainly positive if `n > 0`. Both conditions are satisfied.

So, integrate `n/(n^2 + 1)^2` from `1` to `oo`. Just replace `n` with `x`.

`sum_(n=1)^(oo) n/(n^2 + 1)^2` vs. `int_(1)^(oo) x/(x^2 + 1)^2dx`

Let:
`u = x^2 + 1`
`du = 2xdx`

`=> 1/2int_(1)^(oo) (2x)/(x^2 + 1)^2dx`

`= 1/2int_(1)^(oo) 1/(u^2)du`

`= 1/2 [-1/u]|_a^b`

`=> 1/2 (-1/(x^2+1))|_1^oo`

`= 1/2 [(-1/(oo^2+1)) - (-1/(1^2+1))]`

`= 1/2 [(0) - (-1/(2))] = 1/4`

The integral is finite, and therefore the series converges (`oo^2 = oo, 1/(oo) = 0`).

This is really just using the idea that an integral over an interval is just the accumulation of an infinite number of thin intervals `dn`.