Question

How do you use the intercepts to graph the equation `x-4y= -8`?

Answer 1

The y-intercept is where the line crosses the y-axis, and x = 0. The x-intercept is where the line crosses the x-axis and y = 0. This will give you two points on your line.

Determine the y-intercept, where x = 0.

`0 - 4y = -8`
`-4y = -8`
Divide both sides by -4.
`y = 2`

Determine the x-intercept, where y = 0.

`x - 0y = -8`
`x= -8`

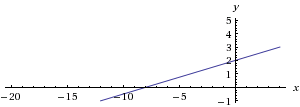
So now you have two points on your line with the y-intercept and x-intercept: (0, 2), representing `(x_1, y_1)`; and (-8, 0), representing `(x_2, y_2)`.

Now that you have two points on the line, you can determine the slope, m, using the equation `m` = `((y_2-y_1))/((x_2-x_1))`.

For this line:

`m` = `((0-2))/((-8-0)) = -2/-8 = 1/4`

The following is a graph of the line showing the y-intercept of 2 and the x-intercept of -8.