Question

How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by `y^2=4x`, x=y revolved about the y-axis?

Answer 1

See below.

Explanation:

Draw a picture (sketch) of the region.
Note that the graphs intersect where `y=x` and `y^2=4x`, so that is where `x^2=4x`.
And that happens at `(0,0)` and at `(4,4)`.

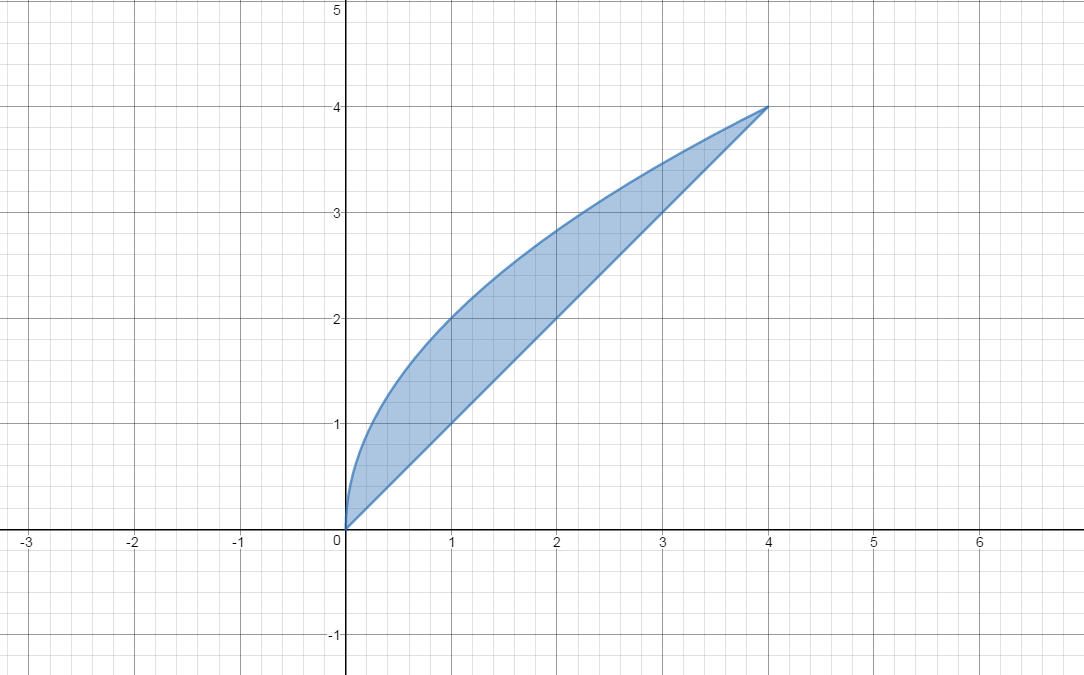
We are asked to use shells, so we take thin representative rectangles parallel to the axis of rotation. In this case that is the `y`-axis.
The slice has solid black boundaries and the radius to the axis of rotation is shown as a dashed black line.

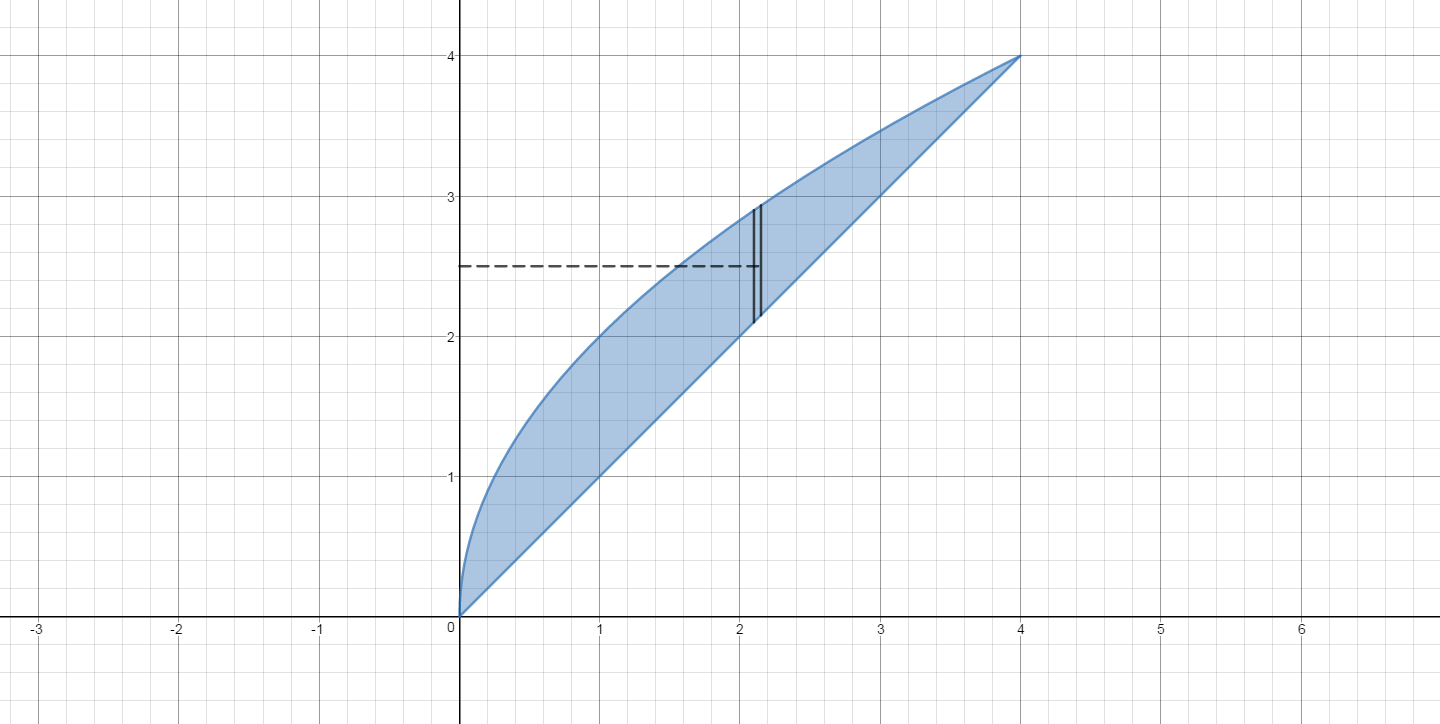
Since the thin part is `dx`, we need both equations as functions of `x`.

`y^2=4x` in the first quadrant (which is where the region is) gets us `y = 2sqrtx` for the upper function.

The lower function is `y=x`

The volume of a representative shell is `2pirh*"thickness"`

In this case, we have

radius `r = x` (the dashed black line),

height `h = upper - lower = 2sqrtx-x` and

`"thickness" = dx`.

`x` varies from `0` to `4`, so the volume of the solid is:

`int_0^4 2pi x(2sqrtx-x)dx =2 piint_0^4 (2x^(3/2)-x^2) dx`

(details left to the student)

`= (128pi)/15`