How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by #y=5x^2#, y=5x revolved about the x-axis?
1 Answer
Please see below.
Explanation:
In order to use shells, we need to take our representative slice parallel to the axis of rotation. So we will take a horizontal slice at a value of
Below is a partial picture. The curves intersect at
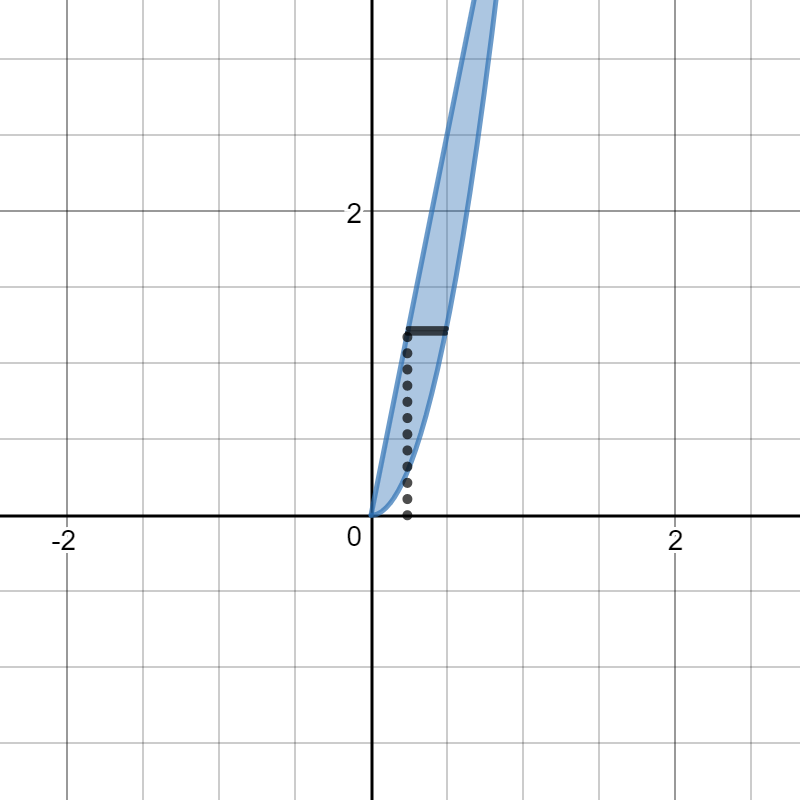
The horizontal slice is shown in black and the radius of revolution is the dotted black line. Its length is
The volume of a representative shell is
In this problem,
The greater
We need to rewrite the equation
The lesser
So the reprentative shell has volume
Details omitted
# = (5pi)/3#

