How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by #y^2=8x# and x=2 revolved about the x=4?
1 Answer
Please see below.
Explanation:
Here is a sketch of the region. To use shells, we'll take a representative slice parallel to the axis of rotation. (Parallel to the line
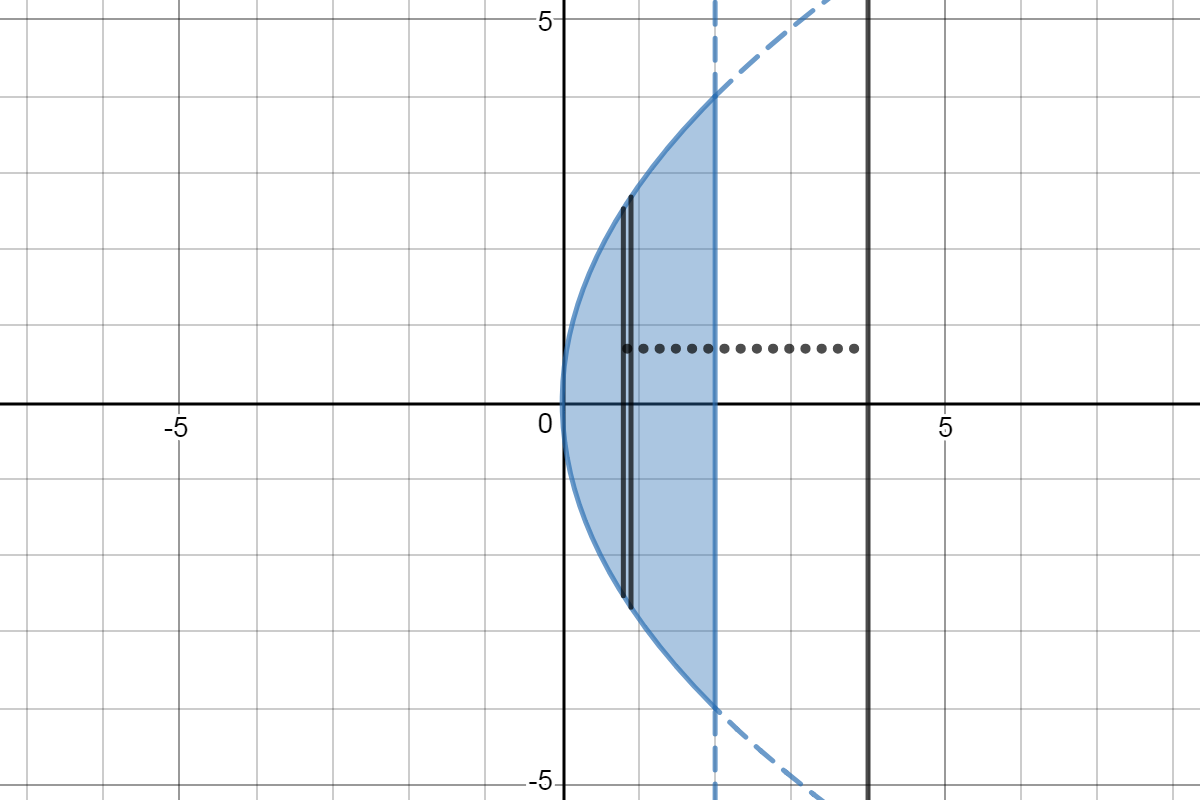
The slice is taken at some value of
The volume of the representative shell is
In this case,
the radius
The height of the slice is the upper
Solving
So,
The volume of the representative shell is
# = 8pisqrt2 int_0^2 (4-x)sqrtx \ dx#
# = 896/15 pi#

