Question

How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by `y =1/(x^2+1)`, x=0, x=1, y=0 revolved about the y-axis?

Answer 1

Volume `= piln2`

Explanation:

If you imagine an almost infinitesimally thin vertical line of thickness `deltax` between the `x`-axis and the curve at some particular `x`-coordinate it would have an area:

`delta A ~~"width" xx "height" = ydeltax = f(x)deltax`

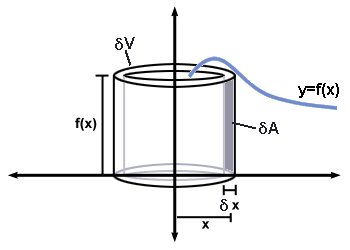
If we then rotated this infinitesimally thin vertical line about `Oy` then we would get an infinitesimally thin cylinder (imagine a cross section through a tin can), then its volume `delta V` would be given by:

`delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax`

If we add up all these infinitesimally thin cylinders then we would get the precise total volume `V` given by:

`V=int_(x=a)^(x=b)2pixf(x) dx`

So for this problem we have:

`V = int_0^1 2pix 1/(x^2+1) dx`
`\ \ \ = pi int_0^1 (2x)/(x^2+1) dx`
`\ \ \ = pi ln|x^2+1)|_0^1`
`\ \ \ = pi (ln2-ln1)`
`\ \ \ = piln2`