How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by #y=8-x^2#, #y=x^2# revolved about the x=2?
1 Answer
Please see below.
Explanation:
In the following picture, the region is shown in blue. The points of intersection of the two curves are
To set up for the method of shells, a slice has been taken parallel to the axis of rotation. The thin side (the thickness of the shell) is
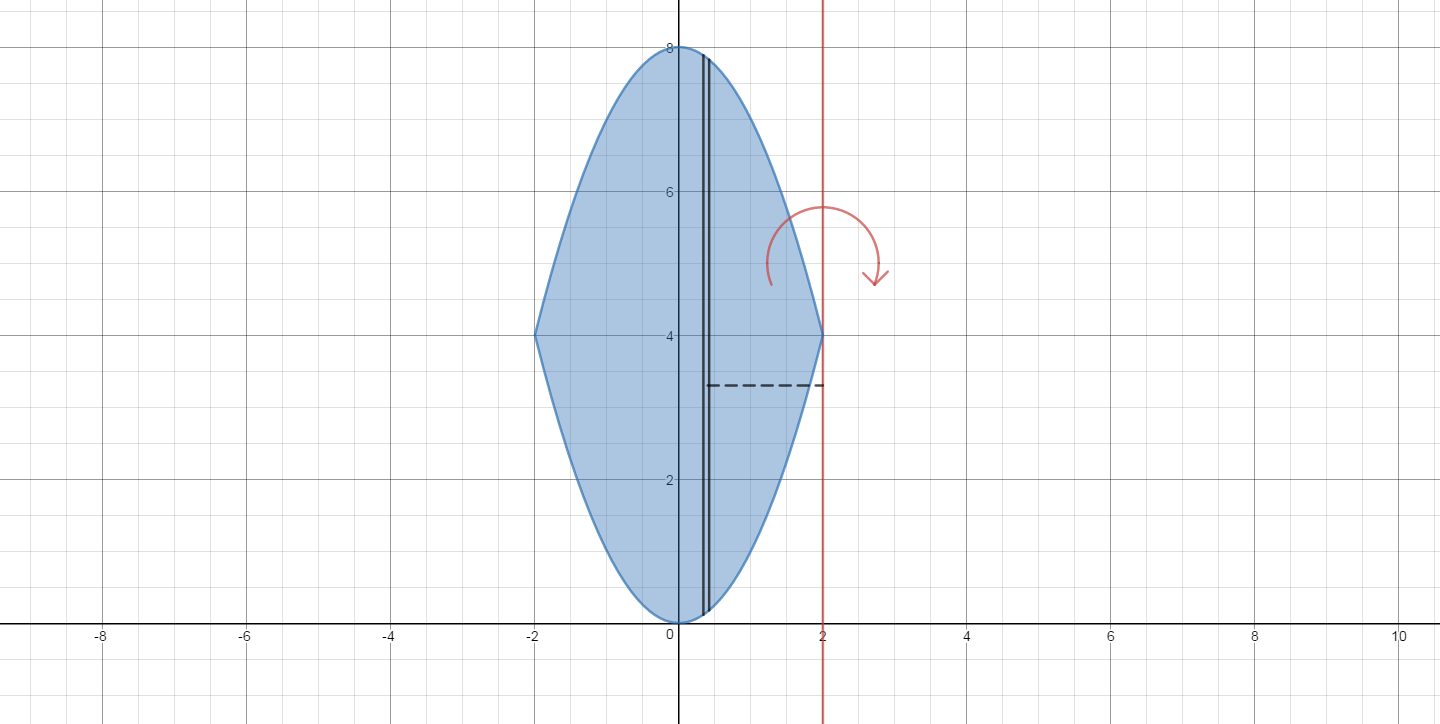
The Volume of a representative shell is
Since the thickness is
(the variable we will work with is
The radius of the shell is
The height is the upper curve minus the lower curve
So the volume of the solid of revolution is
# = 2pi[128/3] = (256 pi)/3#

