How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by #125 y = x^3# , y = 8 , x = 0 revolved about the x-axis?
1 Answer
See below
Explanation:
Here is the region:
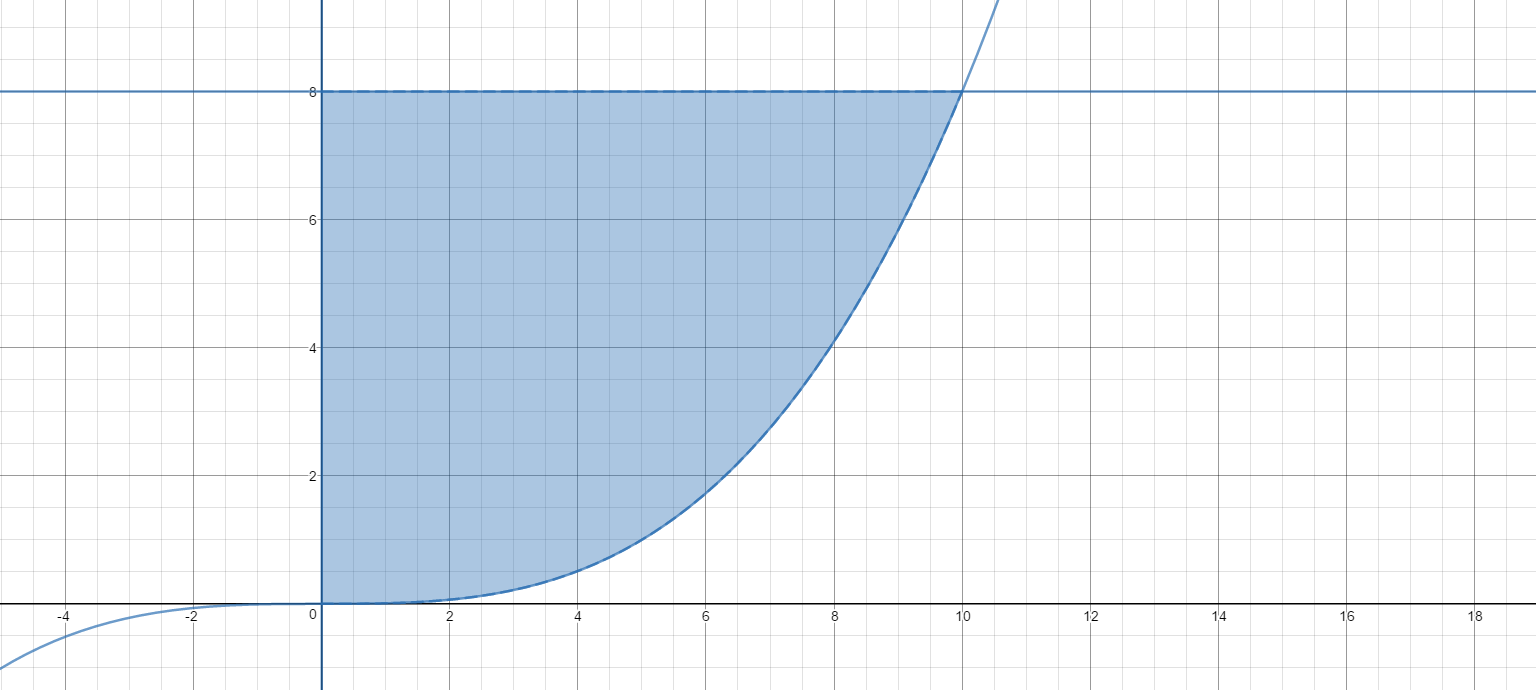
A representative slice taken perpendicular to the axis of rotation has volume
# = pi[640 - 10^7/(7(5^6))]#
# = pi[640 - (10 * 2^6)/7]#
# = pi[640 - 640/7]#
# = pi[(7*640)/7 - 640/7]#
# = pi (6 * 640)/7#
# = (3840pi)/7#
We can also use cylindrical shells to get the same answer:
# V =int_(y=a)^(y=b)2pi \ y \ g(y) \ dy #
# \ \ =2pi int_0^8 \ y \ root(3)(125y) \ dy #
# \ \ =2pi int_0^8 5 \ y \ y^(1/3) \ dy #
# \ \ =10pi int_0^8 y^(4/3) \ dy #
# \ \ =10pi [y^(7/3)/(7/3)]_0^8 #
# \ \ =(30pi)/7 [y^(7/3)]_0^8 #
# \ \ =(30pi)/7 (128-0) #
# \ \ =(3840pi)/7 #


