How do you use the ratio test to test the convergence of the series #∑ 11^n/((n+1)(7^(2n+1)))# from n=1 to infinity?
1 Answer
converges since limit =11/49 < 1
Explanation:
I will use TI screenshots since that's the easiest way to show this stuff.
The Ratio Test says the following:
converges absolutely
if......
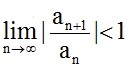
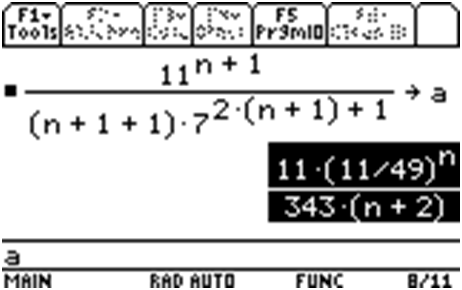
I will do everything internal to the TI89. This saves me lots of time, effort and angst. You will compute the limit of the absolute value of this ratio as
On paper, you need to be attentive to properties of exponents and the simplification of exponential expressions. Also remember that you can pull out (to the left) any constant that appears to the right of the limit operator...in this case, 11/49.
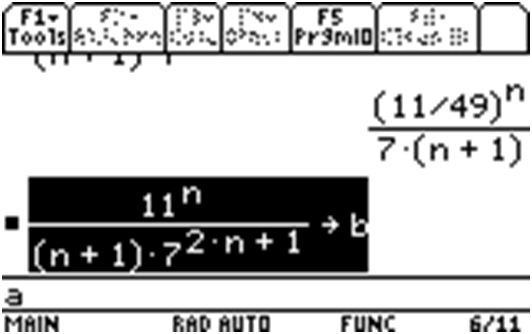
Once you pull out this 11/49, you will arrive at a limit of 1 ( verify this on your own ). It's basically a horizontal asymptote!
So (11/49)(1) = 11/49 < 1 . Hence, you have convergence .
Now, here are the TI screenshots:

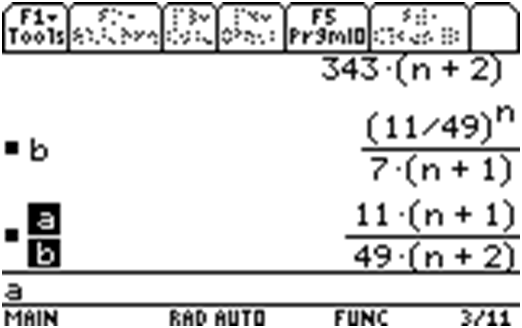
Finally, you can verify this with the actual limit routine for the TI89.
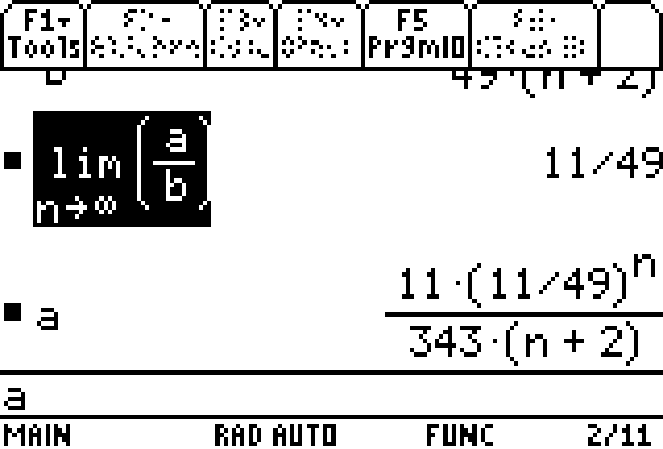
Hope that helps.

