For the equation #color(blue)(2)x^3-x^2+10x-color(red)(5)=0#
any rational roots that exist must be in the set:
#color(white)("XXX"){+- ((color(red)("factors of " 5))/(color(blue)("factors of " 2)))}#
#color(white)("XXX")={ +- ( (color(red)(1,5))/(color(blue)(1,2)) )}#
#color(white)("XXX")={1, 1/2, 5, 5/2, -1, -1/2, -5, -5/2}#
Using synthetic substitution with these candidate values:
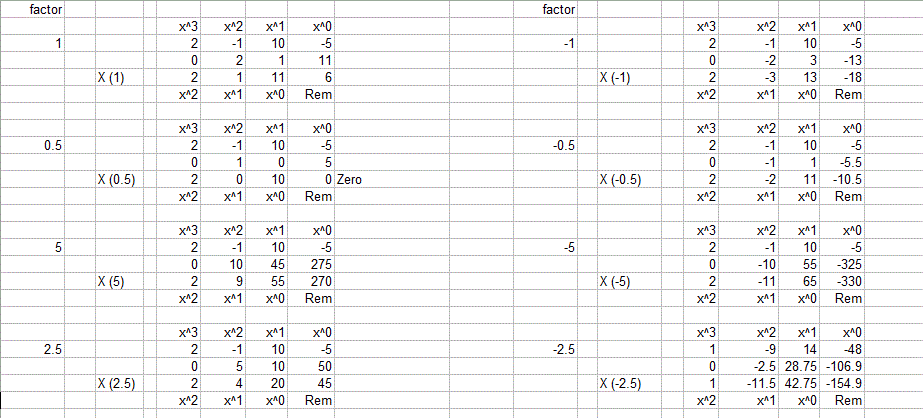
We find the only rational root is #x=1/2#
and that #2x^3-x^2+10x-5=0# can be factored as
#color(white)("XXX")(x-1/2)(2x^2+10)=0#
The #(x-1/2)=0# gave us the root #x=1/2#
but if #(2x^2+10)=0# is to give us any further roots:
#color(white)("XXX")2x^2=-10#
#color(white)("XXX")x^2=-5#
#color(white)("XXX")x=+-sqrt(-5)#
#color(white)("XXX")x=+-isqrt(5)#
