How do you use the rational root theorem to find the roots of #x^4-x^3-2x^2-4x-24#?
1 Answer
Use rational root theorem to find possible rational zeros. Try the first few, then use synthetic division with the roots found to find there are no more Real ones.
Explanation:
Let
By the rational root theorem, any rational roots of
So the only possible rational roots are:
Let us try a few:
So
Use synthetic division:
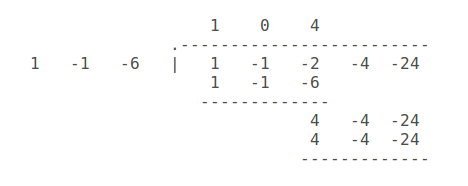
So

