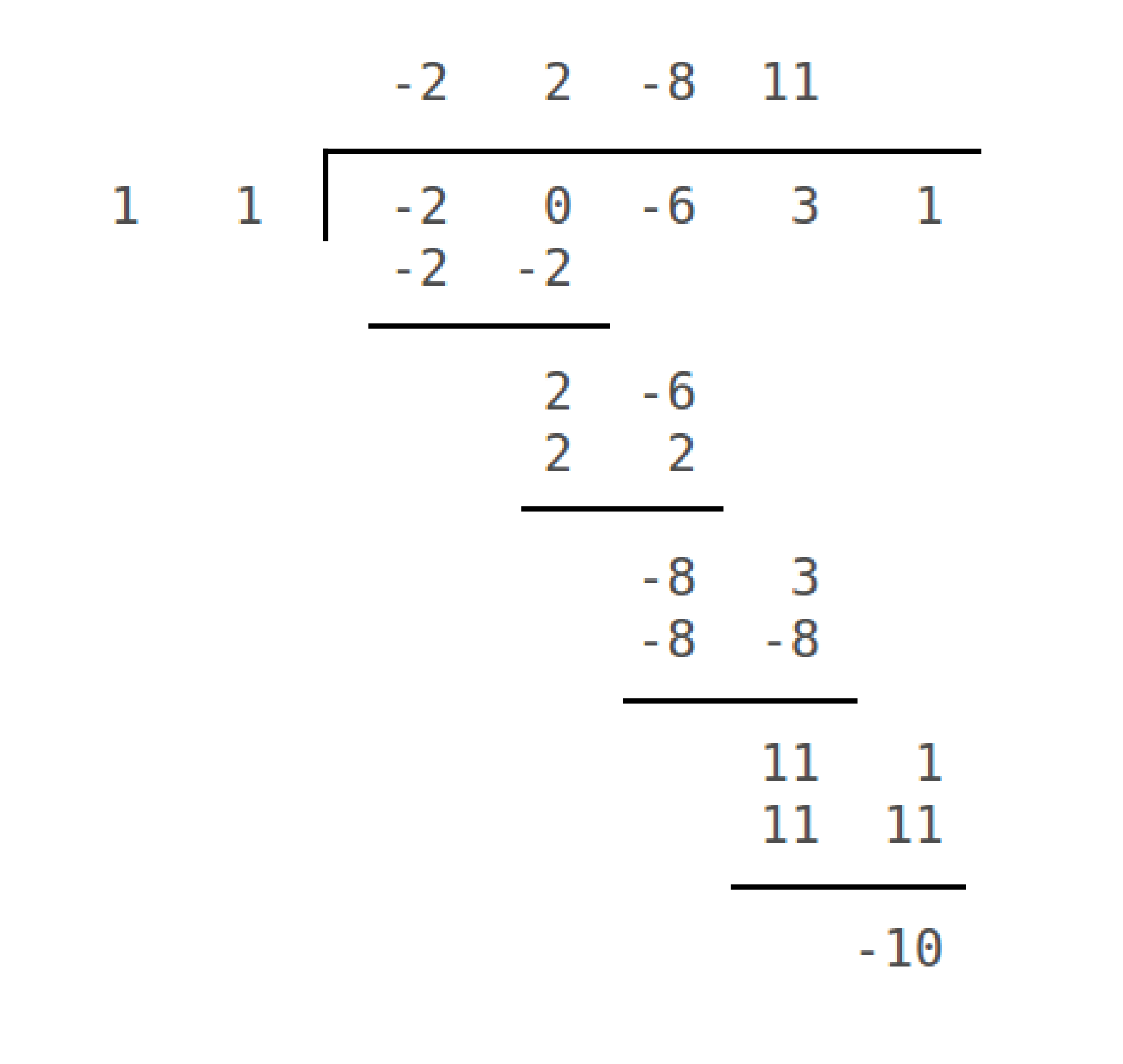How do you use the remainder theorem and Synthetic Division to find the remainders in the following division problems #-2x^4 - 6x^2 + 3x + 1 # divided by x+1?

Question

2436 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-07-30T20:14:36

Let #f(x) = -2x^4-6x^2+3x+1#.

Using the remainder theorem, the remainder is

#f(-1) = -2-6-3+1 = -10#

Using Synthetic division we get the same remainder.

The remainder theorem states that the remainder of dividing a polynomial #f(x)# by #(x-a)# is #f(a)#. In our case #a=-1# and #f(-1) = -10#.

Alternatively, using synthetic division we get the same remainder...

Here we divide #-2x^4-6x^2+3x+1# by #x+1#. Note the #0# in #-2, 0, -6, 3, 1#, standing for the missing #x^3# term's coefficient.

enter image source here