How do you use the remainder theorem to determine the remainder when the polynomial #x^4+x^3-5x^2+2x-7# is divided by #x+2#?

Question

1330 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-23T16:17:28

The remainder is the result of substituting #x=-2#, namely #-23#

#f(x) = x^4+x^3-5x^2+2x-7#

The remainder when divided by #(x-a)# is #f(a)#.

So the remainder when divided by #(x+2)# is:

#f(-2) = 16-8-20-4-7 = -23#

Here is a long division of the coefficients, just to check:

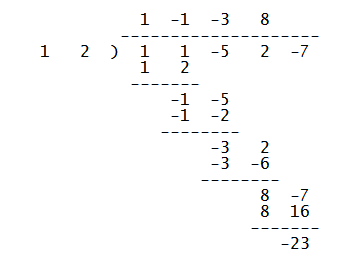
enter image source here

So:

#x^4+x^3-5x^2+2x-7 = (x^3-x^2-3x+8)(x+2)-23#