How do you use the shell method to compute the volume of the solid obtained by rotating the region in the first quadrant enclosed by the graphs of the functions #y=x^2# and #y=2# rotated about the y-axis?

Question

19596 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-02-22T15:08:05

We will rotate the area bounded by the two curves and the y-axis. In other words we will restrict ourselves to the region in the first quadrant.

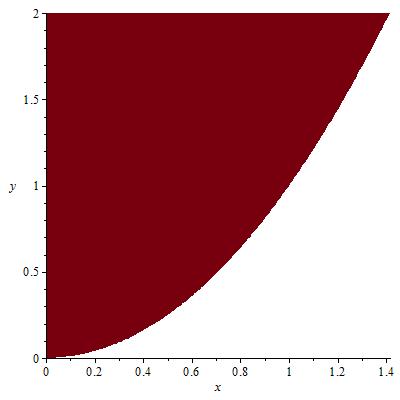
enter image source here

Since we a rotating around the y axis using the method of shells
we integrate with respect to x.

Now find where the curves intersect.

#x^2=2 #

#x=+-sqrt{2} # We use positive square root since we are in quadrant I

Therefore the interval over which we integrate is #0<=x<=sqrt{2} #

Our representative radius will be some value of #x# over this interval.

Our representative cylinder height is #2-x^2#.

Using method of shells, the integral for the volume is

#2piint_0^sqrt{2}x(2-x^2)dx#

#2piint_0^sqrt{2}2x-x^3dx #

Now integrate

#2pi(x^2-x^4/4) #

#2pi((sqrt{2})^2-((sqrt{2})^4)/4-0) #

#2pi(2-1)=2pi(1)=2pi #