Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region `y=4-x^2` and `y=0` rotated about the y-axis?

Answer 1

See the explanation, below.

Explanation:

Here is the region with a thin slice taken parallel to the axis of rotation. (To set up for cylindrical shells.)

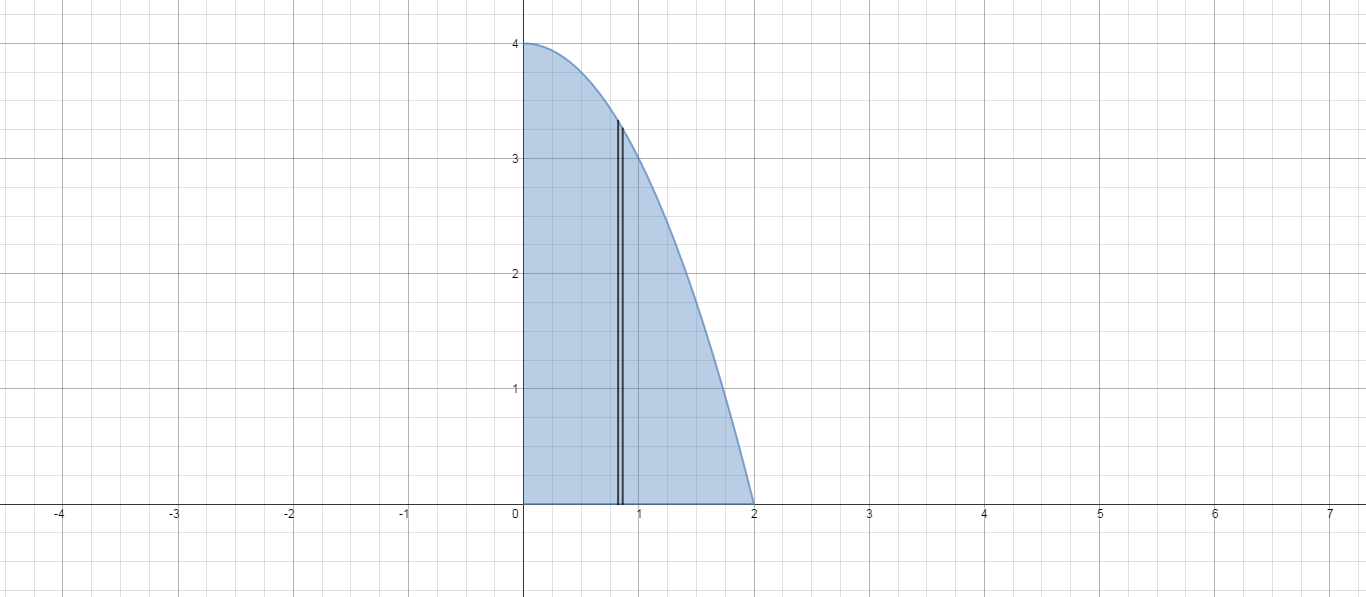
The volume of a representative shell is `2pirh*"thickness"`

In this case, we have radius `r = x`, height `h = 4-x^2` and `"thickness" = dx`. `x` varies from `0` to `2`, so the volume of the solid is:

`int_0^2 pi x(4-x^2)dx = piint_0^2 (4x-x^3) dx = 4pi`