How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #y = sqrt(x#), #y = 0#, #y = 12 - x# rotated about the x axis?
1 Answer
Volume =
Explanation:
If you imagine an almost infinitesimally thin vertical line of thickness
#delta A ~~"width" xx "height" = ydeltax = f(x)deltax#
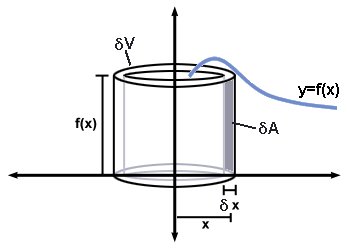
If we then rotated this infinitesimally thin vertical line about
#delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax#
If we add up all these infinitesimally thin cylinders then we would get the precise total volume
# V=int_(x=a)^(x=b)2pi \ x \ f(x) \ dx #
Similarly if we rotate about
# V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy #
So for this problem we have:
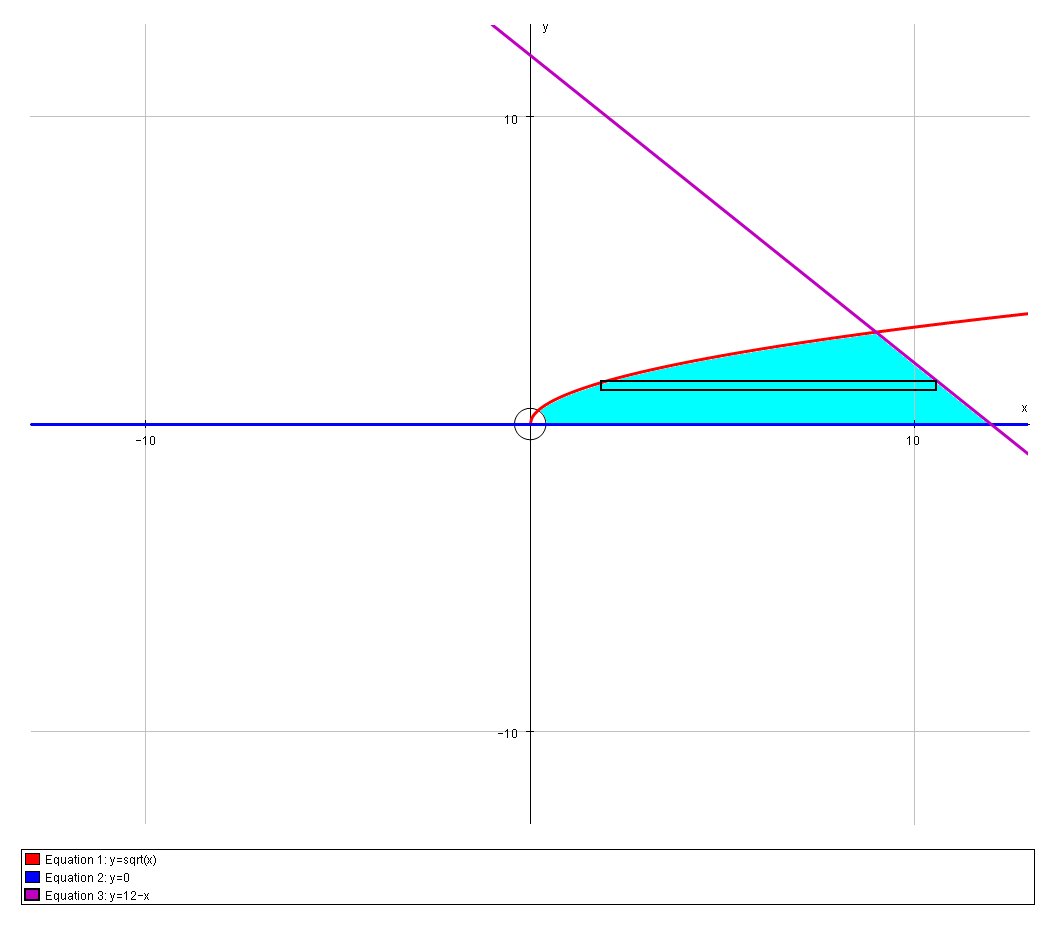
We need the point of intersection for the bounds of integration;
# 12-x = sqrt(x) => (12-x)^2 =x #
# :. 144-24x+x^2=x #
# :. x^2 - 25x + 144 =0 #
# :. (x-9)(x-16) =0 => x=9,16 #
And our solution is
# x=9 => y=12-x = 3 #
So the bounding curves
And we also need
# y=12-x => x=12-y #
# y = sqrt(x) \ \ \ \ \ => x=y^2 #
Then the required volume is given by:
# V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy #
# \ \ \= 2pi int_(y=0)^(y=3) \ y{(12-y) - (y^2)} \ dy #
# \ \ \= 2pi int_(y=0)^(y=3) \ y(12-y - y^2) \ dy #
# \ \ \= 2pi int_(y=0)^(y=3) \ 12y-y^2 - y^3) \ dy #
# \ \ \= 2pi [ 6y^2 - 1/3y^3 - 1/4y^4 ]_0^3 #
# \ \ \= 2pi (54-9-81/4) #
# \ \ \= (99pi)/2 #

