Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region `y=6x+7` and `y=x^2` rotated about the line `y=49`?

Answer 1

Given a choice, I would use washers, but. . .

Explanation:

Here is a (non-interactive) graph using Desmos (desmos.com)
I have included the line `y=49` in red.

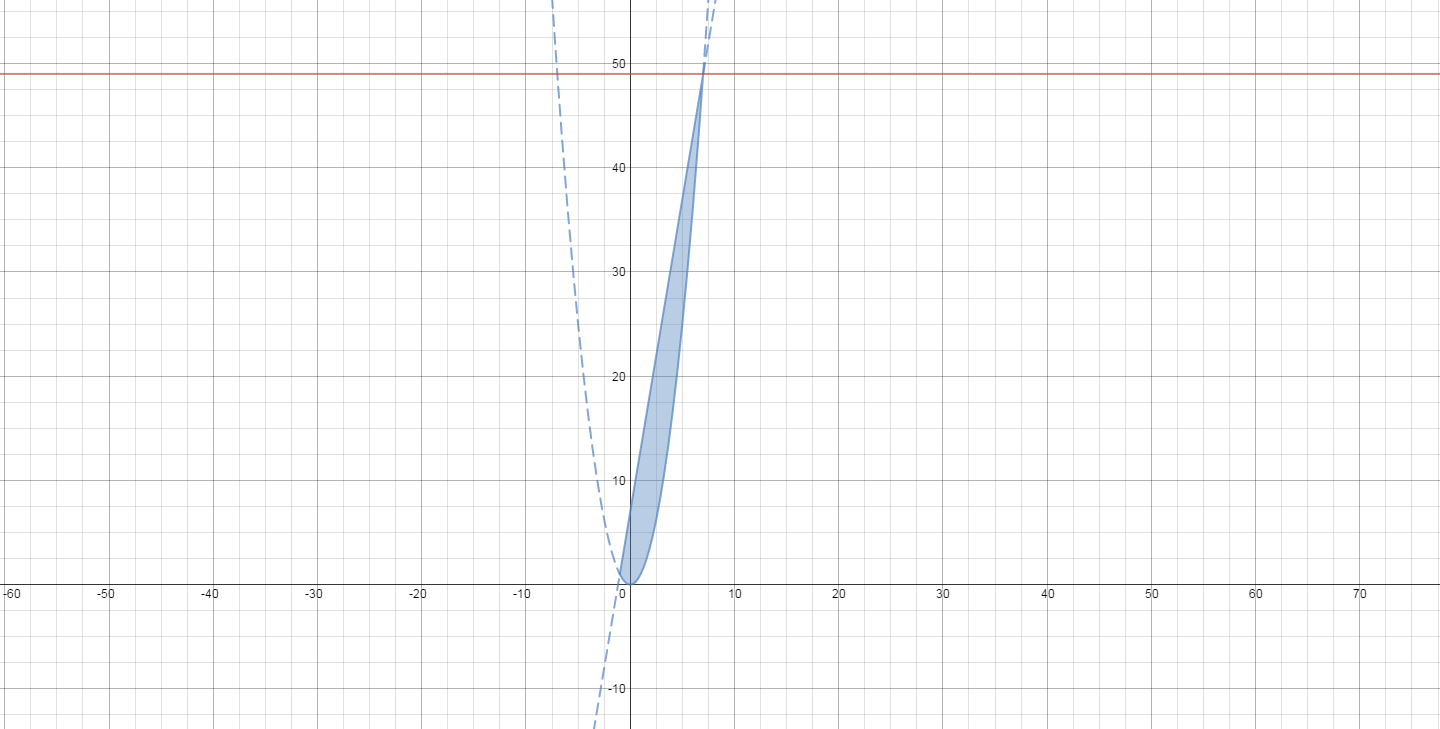
Here is the region using the Socratic grapher. It isn't quite accurate, but you can zoom in and out and drag the graph around

graph{(y-x^2)(y-6x-7) (sqrt(x+1))/(sqrt(x+1))<= 0 [-8.29, 20.21, -6, 8.26]}

`y=6x+7` if and only if `x=1/6y-7/6`

`y=x^2` if and only if `x= +-sqrty`

To use shells we take our representative slices horizontally. So the bounds become

For `y=0` to `y=1`, `x` goes from `-sqrty` to `sqrty`.

From `y-1` to `y=49`, `x` goes from `1/6y-7/6` to `sqrty`.

Throughout the problem, the radius of the cylindrical shell will be `49-y`

So we need to evaluate two integrals:

`2pi int_0^1 (49-y)(sqrty-(-sqrty))dy = 4pi int_0^1 (49y^(1/2)-y^(3/2))dy`

`= 1936/15pi`

And

`2pi int_1^49 (49-y)(sqrty-(1/6y-7/6))dy = 25296/5pi`

The volume is the sum of the two integrals.

Washers

`pi int_-1^7 [(49-x^2)^2-(49-(6x+7))^2]dx = 77824/15pi`