It's unclear what your solid is, but the only one that makes sense is #y = sqrt2# and not #y = 0# because #y = 0# is redundant when you are rotating about the x-axis. Maybe you meant to emphasize that it is #y = sqrtx# and not #y = -sqrtx#. Assuming that:
#x = y^2 -> y = sqrtx#
You only need the positive one since #y = 0# is a boundary, and is also your axis of rotation. Thus, you are looking at this:
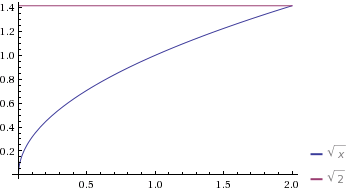
Since the shell method implies you are rotating about the y-axis (which is inconvenient for the regular revolution method), we can rewrite this for that.
#x = y^2 -> y = x^2 in [0, oo)# (only positive #x#)
#y = 0 -> x = 0#
#y = sqrt2 -> x = sqrt2#
Now we really just have #y = x^2# in the first quadrant rotated around the y-axis, stopped at #x = sqrt2#, intersecting at #(sqrt2, 2)#. Which is:
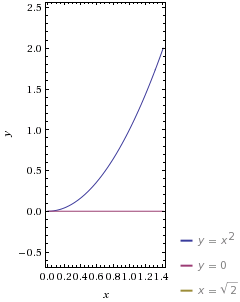
The shell method is:
#int_a^b 2pixf(x)dx#
where:
#2pi# is the radian measure for the "circumference" of the shape
#x# is the radius of the shell
#f(x)# is the height of the shell
#V = 2piint_0^sqrt2 x(x^2)dx#
#= 2pi (x^4/4)|_(0)^sqrt2#
#= 2pi ((sqrt2)^4/4 - 0^4/4)#
#= 2pi (1)#
#= color(blue)(2pi "rad")#

