How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #y= sqrt(5x)#, #x=5# rotated about the y axis?
1 Answer
Please see the explanation section, below.
Explanation:
The region bounded by the functions is shown below in blue.
We are using the shell method, so we take a representative slice parallel to the axis of revolution. In this case, that is the
The dashed line shows the radius of revolution for the representative.
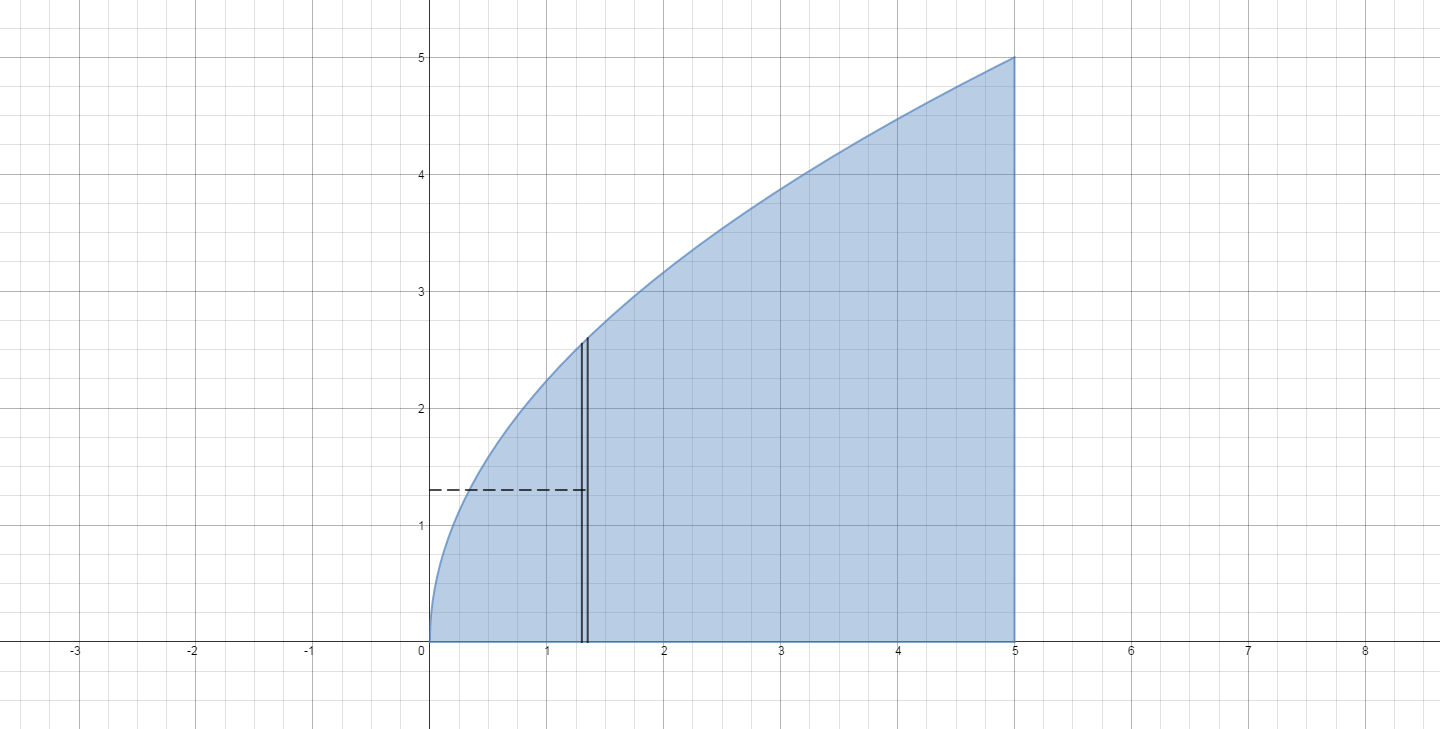
We will be integrating with respect to
From the given information, we conclude that
The volume of a cylindrical shell is the surface area of the cylinder times the thickness:
In the picture, the radius is shown by the dashed line, it is
The height of the slice is the upper
The volume of the representative shell is:
The volume of the resulting solid is:
# = 2pisqrt5 int_0^5 x^(3/2)dx#
# = 2pisqrt5[(2x^(5/2))/5]_0^5= 100pi#

