How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #y=sqrt(16-x^2)# and the x axis rotated about the x axis?
1 Answer
Volume
Explanation:
If you imagine an almost infinitesimally thin vertical line of thickness
#delta A ~~"width" xx "height" = ydeltax = f(x)deltax#
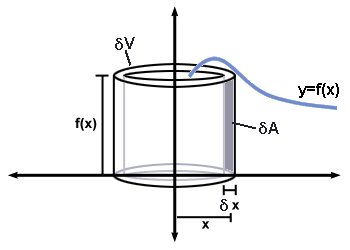
If we then rotated this infinitesimally thin vertical line about
#delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax#
If we add up all these infinitesimally thin cylinders then we would get the precise total volume
# V=int_(x=a)^(x=b)2pi \ x \ f(x) \ dx #
Similarly if we rotate about
# V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy #
So for this problem we have:
graph{(y-sqrt(16-x^2))=0 [-8, 8, -2, 5]}
We need the point of intersection for the bounds of integration;
# sqrt(16-x^2) = 0 => x =+- 4 # , and the range of#y# is#y in [-4,4]#
By symmetry we can restrict
# y=sqrt(16-x^2) => y^2=16-x^2 => x=sqrt(16-y^2)#
The Volume of Revolution about
# 1/2V = int_(y=a)^(y=b)2pi \ y \ g(y) \ dy #
# \ \ \ \ \ \ = int_(y=0)^(y=4)2pi \ y \ sqrt(16-y^2) \ dy #
# \ \ \ \ \ \ = 2pi \ int_0^4 y \ sqrt(16-y^2) \ dy #
We can use a substitution to perform this integral;
Let
#u=16-y^2 => (du)/(dy)= -2y #
When# { (y=-4), (y=4) :} => { (u=16), (u=0) :} #
Substituting into the integral we get:
# 1/2V = 2pi \ int_16^0 \ sqrt(u) (-1/2)\ du #
# \ \ \ \ \ \ = pi \ int_0^16 \ sqrt(u) \ du #
# \ \ \ \ \ \ = pi \ [u^(3/2)/(3/2)]_0^16 #
# \ \ \ \ \ \ = 2/3pi \ [u^(3/2)]_0^16 #
# \ \ \ \ \ \ = 2/3pi \ (16^(3/2) - 0) #
# \ \ \ \ \ \ = (128pi)/3 #
# :. V = (256pi)/3 #
Note:
The volume is that of a sphere of radius

