How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #x= y^2# #x= y+2# rotated about the y-axis?
1 Answer
See explanation below.
Explanation:
To use shells when revoling about a vertical line, we need to take our representative slices vertically, so the thickness is
Here is a picture of the region to be revolved about the
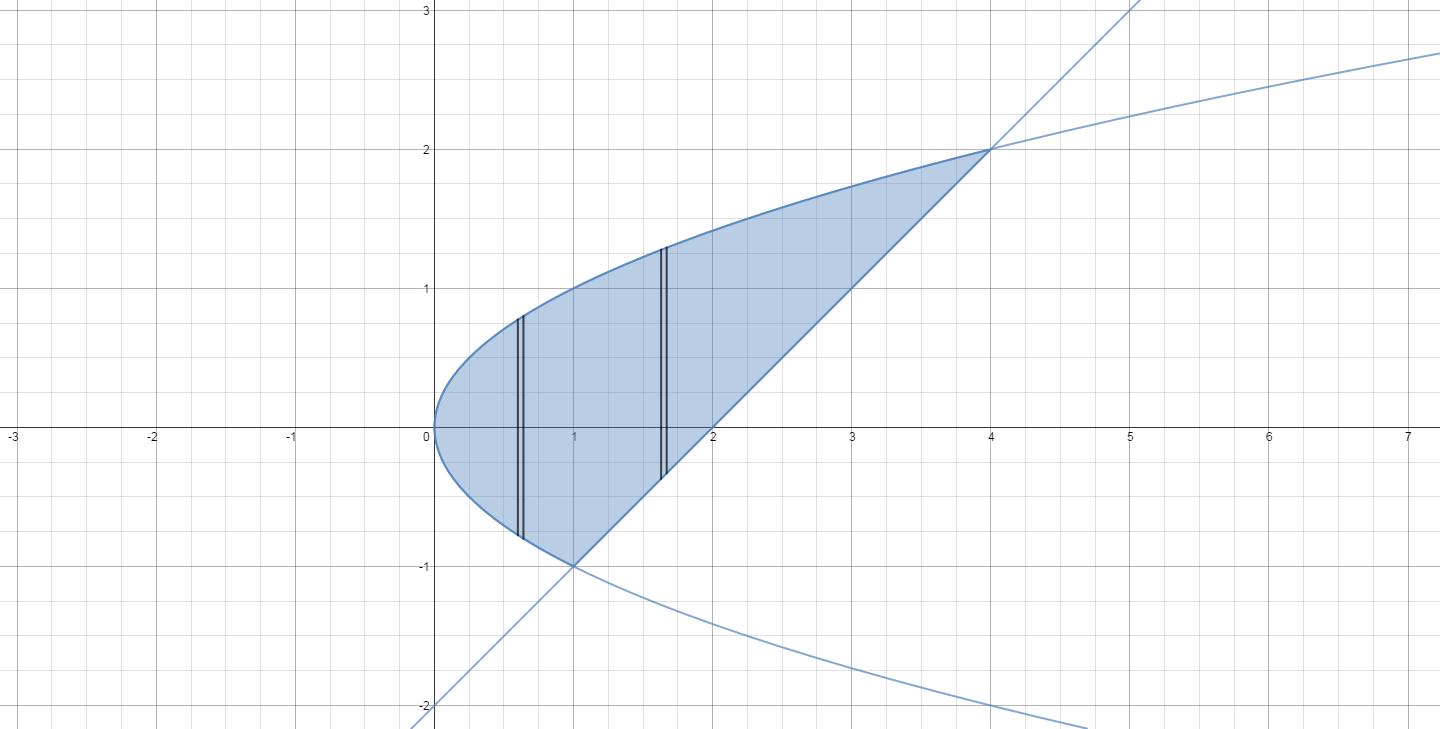
The curves intersect at
The radii of our cylindrical shells will be
The thickness is
the height of each shell is the greater
(The
The greater value of
The lesser value of
From
To get that part of the volume, we need to evaluate:
From
To get that part of the volume, we need to evaluate:
The total volume is found by adding these two results, to get:

