How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region $x = y - y^{2}$ $x=y-y^2$ and the y axis rotated about the y axis?

Question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region $x = y - y^{2}$ $x=y-y^2$ and the y axis rotated about the y axis?

1 Answer

Impact of this question

2485 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-10-25T14:41:29

See the explanation section, below.

Explanation:

Here is a picture of the region. Because we have been asked to ue shells, a representative slice has been taken parallel to the axis of revolution. This make the thickness of our slice $d x$ $dx$

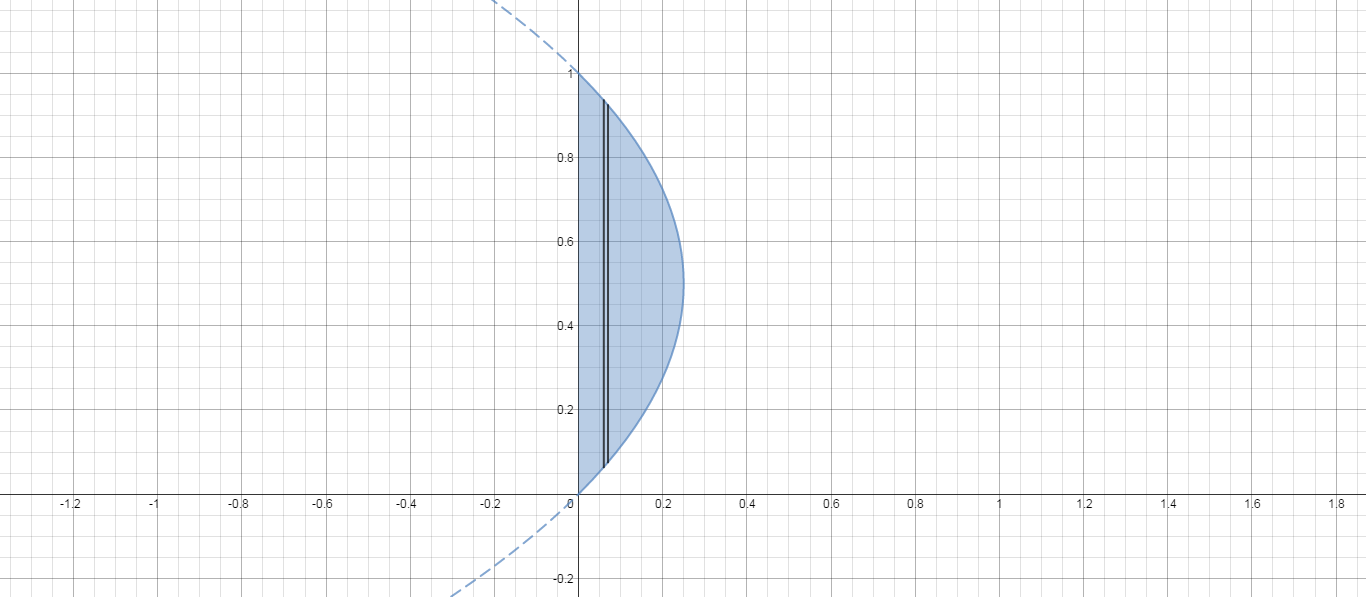
enter image source here

The volume of the representative shell is:

$2 π \times radius \times height \times thickness$ $2 pixx "radius"xx"height"xx"thickness"$

As mentioned, $thickness = d x$ $"thickness" = dx$
and we can see that $radius = x$ $"radius"=x$

The $height$ $"height"$ will be the greater $y$ $y$ value minus the lesser $y$ $y$ value. We are working in terms of $x$ $x$ , so we need to write these two $y$ $y$ values as functions of $x$ $x$ .

We need to solve $x = y - y^{2}$ $x=y-y^2$ for $y$ $y$ (in terms of $x$ $x$ ).

There are a couple of ways of doing this. (1) complete the square or (2) use the quadratic formula to solve $y^{2} - y + x = 0$ $y^2-y+x=0$ for $y$ $y$ .
(There are other ways as well. For example, you can use the vertex formula to write the equation in standard form for a sideways opening parabola.)

I'll complete the square.

$y^{2} - y = - x$ $y^2-y = -x$

$y^{2} - y + \frac{1}{4} = \frac{1}{4} - x$ $y^2-y +1/4 = 1/4-x$

${(y - \frac{1}{2})}^{2} = \frac{1 - 4 x}{4}$ $(y-1/2)^2 = (1-4x)/4$

$y - \frac{1}{2} = \pm \sqrt{\frac{1 - 4 x}{4}}$ $y-1/2 = +-sqrt((1-4x)/4)$

$y = \frac{1}{2} \pm \frac{\sqrt{1 - 4 x}}{2} = \frac{1 \pm \sqrt{1 - 4 x}}{2}$ $y = 1/2+-sqrt(1-4x)/2 = (1+-sqrt(1-4x))/2$

(Yes, this is the same as the answer you'll get by using the quadratic formula.)

The greater $y$ $y$ (the one on top) is
$y_{top} = \frac{1 + \sqrt{1 - 4 x}}{2}$ $y_"top" = (1+sqrt(1-4x))/2$

and the lesser $y$ $y$ (the one on the bottom) is
$y_{bottom} = \frac{1 - \sqrt{1 - 4 x}}{2}$ $y_"bottom" = (1-sqrt(1-4x))/2$

So, finally, we can write the volume of the representative cylindrical shell:

$2 π \times radius \times height \times thickness = 2 π x (\frac{1 + \sqrt{1 - 4 x}}{2} - \frac{1 - \sqrt{1 - 4 x}}{2}) d x$ $2 pixx "radius"xx"height"xx"thickness" = 2pix((1+sqrt(1-4x))/2-(1-sqrt(1-4x))/2) dx$

Don't Panic. We can simplify this to get

$2 π x \sqrt{1 - 4 x} d x$ $2pixsqrt(1-4x)dx$

We still haven't found the bounds on $x$ $x$ .

In the region we have $0 \leq x$ $0 <= x$ , and, examining the solution for $y$ $y$ , we see that if $x > \frac{1}{4}$ $x > 1/4$ we'll get imaginary values for $y$ $y$ . So, we get $x$ $x$ varies from $0$ $0$ to $\frac{1}{4}$ $1/4$ .

The volume of the solid of interest is

$V = \int_{0}^{\frac{1}{4}} 2 π x \sqrt{1 - 4 x} d x$ $V = int_0^(1/4) 2 pi x sqrt(1-4x) dx$

Which can be evaluated by parts or by the substitution $u = 1 - 4 x$ $u = 1-4x$ so that $d u = - 4 d x$ $du = -4 dx$ and $x = \frac{1}{4} (1 - u)$ $x = 1/4(1-u)$ .

Science

Math

Humanities

... and beyond

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region $x = y - y^{2}$ $x=y-y^2$ and the y axis rotated about the y axis?

1 Answer

Explanation:

Related questions

Impact of this question

Science

Math

Humanities

... and beyond

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region x=y−y2x=y-y^2 and the y axis rotated about the y axis?

1 Answer

Explanation:

Related questions

Impact of this question

How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region $x = y - y^{2}$ $x=y-y^2$ and the y axis rotated about the y axis?