How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #y=2-x#, #2<=x<=4# rotated about the x-axis?
1 Answer
Oct 9, 2015
Always graph the constraints first, then determine the correct integration formula.
Explanation:
Here is a graph of the constraints:
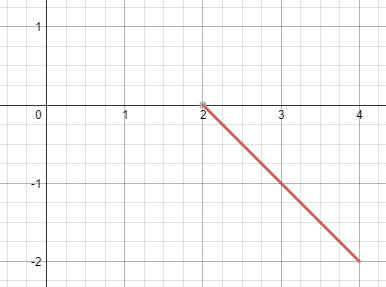
Now, without using calculus, you should visualize rotating this line around the x-axis will generate a cone with radius 2 and height 2. The volume of a cone is:
So, in advance of using calculus, we know the answer is
Now, using calculus and the shell method :
Because we rotate around the x-axis, integrate with respect to y:
hope that helped

