How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region #y = sqrt(x)#; #y = 0#; and #x = 4# rotated about #y=6#?
1 Answer
Sep 26, 2015
See the explanation section below.
Explanation:
Here is a picture of the region and the line
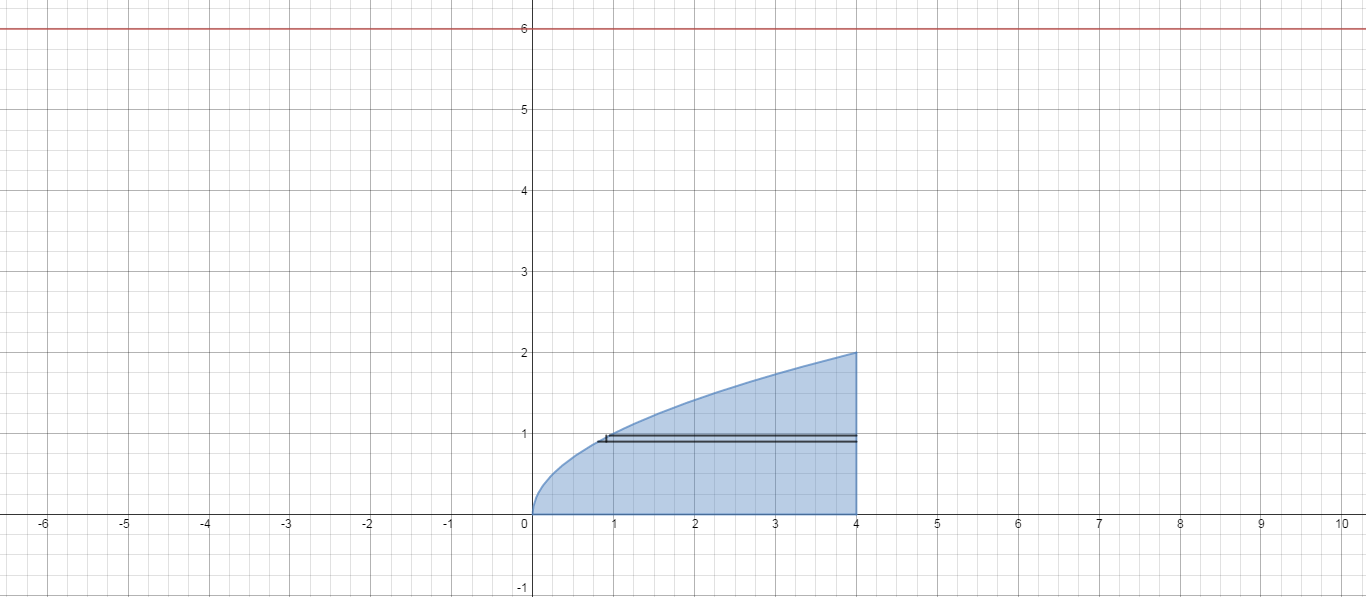
I've tried to show a representative slice to use cylindrical shells.
The thickness of the shell is
The curve
In the region,
At each value of
and the 'height' of the shell (it is lying on its side) will be the greater
The volume of a representative shell is
So we need to integrate:
Expand the polynomial and integrate term by term to get

