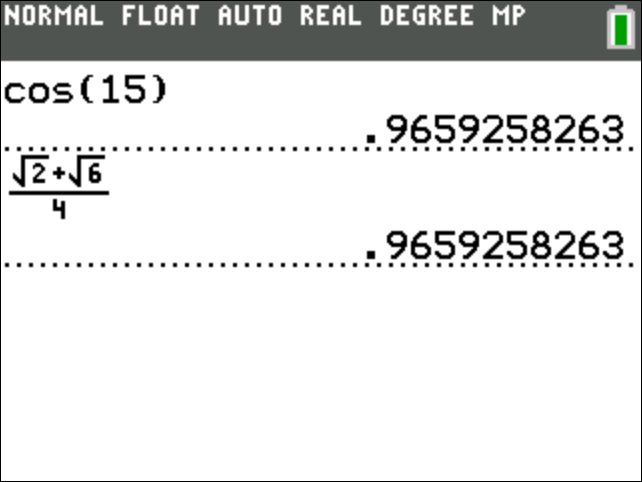
How do you use the sum and difference identities to find the exact value of #cos 15^@#?
1 Answer
Oct 24, 2014
The special triangles, 30-60-90 and 45-45-90, allow us to evaluate sin and cos.
We leverage that information to evaluate
Verify your results using a calculator. Make sure the calculator is in Degree Mode.