How do you use the summation formulas to rewrite the expression #Sigma (2i+1)/n^2# as i=1 to n without the summation notation and then use the result to find the sum for n=10, 100, 1000, and 10000?
1 Answer
Explanation:
Let
# S_n = sum_(i=1)^n (2i+1)/n^2 #
# :. S_n = 1/n^2sum_(i=1)^n (2i+1) #
# :. S_n = 1/n^2{2sum_(i=1)^n (i)+sum_(i=1)^n (1)} #
And using the standard results:
We have;
# \ \ \ \ \ S_n = 1/n^2{2*1/2n(n+1) + n} #
# :. S_n = 1/n^2{n(n+1) + n} #
# :. S_n = 1/n^2{n^2+n + n} #
# :. S_n = 1/n^2{n^2+2n} #
# :. S_n = 1/n^2{n(n+2)} #
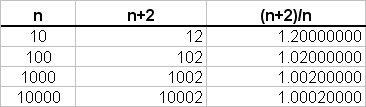
# :. S_n = (n+2)/n #
And this has been calculated using Excel for

What happens as
[ NB As an additional task we could possibly conclude that as
Now,
# :. S_n = 1+2/n #
And so,
# lim_(n rarr oo) S_n = lim_(n rarr oo) (1+2/n) #
# :. lim_(n rarr oo) S_n = lim_(n rarr oo) (1) + 2lim_(n rarr oo)(1/n) #
# :. lim_(n rarr oo) S_n = 1+0 #
# :. lim_(n rarr oo) S_n = 1#
Which confirms our assumption!

