Question

How do you use the trapezoid rule to approximate the equation `y=x^2 -2x +` bounded by `y=0`, `x=0`, and `x=3`?

Answer 1

Evaluate `y=x^2-2x` for `x epsilon {0, 1, 2, 3}`; calculate the areas between adjacent `x` values and sum the areas to get an approximation (3.5 sq. units)

Explanation:

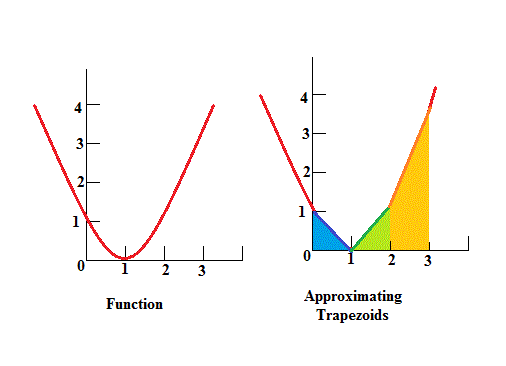
(See diagram of the function graph and approximating trapezoids below).

Area of each trapezoid
`color(white)("XXXX")` `= "width" xx ("height at " x_1 + "height at " x_2)/2`
`color(white)("XXXX")` `color(white)("XXXX")`(in this case the `"width" = 1` for all trapezoids).

`"Area"_(0:1) = 1 xx(1+0)/2 = 1/2`

`"Area"_(1:2) = 1xx(0+1)/2 = 1/2`

`"Area"_(2:3) = 1xx (1+4)/2 = 2 1/2`

Total Area of the 3 Trapezoids (which approximate area under the curve)
`color(white)("XXXX")` `= 1/2 + 1/2 + 2 1/2 = 3 1/2`

`color(white)("XXXX")` `color(white)("XXXX")` `...that's`3+1/2`or`3.5# for our friends in France who have never seen mixed fractions before ; )