How do you use the Trapezoidal Rule to approximate integral #int(2/x) dx# for n=4 from [1,3]?
1 Answer
Jun 25, 2018
# int_1^3 \ 2/x \ dx ~~ 2.233333#
Explanation:
We have:
# y = 2/x #
We want to estimate
# Deltax = (3-1)/4 = 0.5#
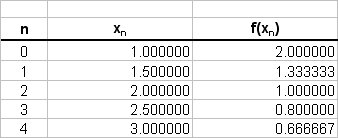
The values of the function are tabulated as follows;
Trapezium Rule
# A = int_a^b \ y \ dx #
# \ \ \ ~~ h/2{y_0+y_n+2(y_1+...+y_(n-1)) } #
# \ \ \ = 0.5/2 * { 2 + 0.666667 + 2*(1.333333 + 1 + 0.8) } #
# \ \ \ = 0.25 * { 2.666667 + 2*(3.133333) }#
# \ \ \ = 0.25 * { 2.666667 + 6.266667 }#
# \ \ \ = 0.25 * 8.933333#
# \ \ \ = 2.233333#
Actual Value
For comparison of accuracy:
# A = int_1^3 \ 2/x \ dx #
# \ \ \ = [2lnx]_1^3 #
# \ \ \ = 2ln3-2ln1 #
# \ \ \ = 2ln3 #
# \ \ \ ~~ 2.1972 #