Question

How do you use the trapezoidal rule with n=4 to approximate the area between the curve `(5t + 6)` from 3 to 6?

Answer 1

`int_(3)^(6) 5t+6 \ dt =85.5`

Explanation:

The required area is a trapezium with sides `21` and `36` and width `3`, so we can calculate the exact area as `A=1/2(21+36)3 = 85.5`. As the trapezium rule estimates the area under a curve using trapeziums we would expect to get an exact answer.

The values of `f(x)=5x+6` are tabulated as follows (using Excel) working to 5dp

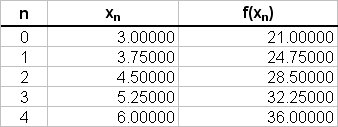
Using the trapezoidal rule:

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

We have:

`int_(3)^(6) 5t+6 \ dt ~~ 0.75/2 { 21 + 36 + 2(24.75 + 28.5 + 32.25)}`
`" " = 0.375 { 57 + 2( 85.5 )}`
`" " = 0.375 { 57 + 171 }`
`" " = 0.375 { 228 }`
`" " = 85.5 " "`, as predicted