How do you use the trapezoidal rule with n=4 to approximate the area between the curve #sqrt(x) sinx# from pi/2 to pi?

1 Answer
Steve M
Nov 9, 2016

# int_(pi/2)^pisqrt(x)sinxdx ~~ 1.430 # (3dp)

Explanation:

The values of y are tabulated as follows (using Excel)

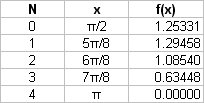
enter image source here

Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#

we have:
# int_(pi/2)^pisqrt(x)sinxdx ~~ (pi/8)/2{ (1.25331 + 0.00000) + 2(1.29458 + 1.08540 + 0.63448)} #
# :. int_(pi/2)^pisqrt(x)sinxdx ~~ pi/16{ 1.25331 + 2(3.01446)} #
# :. int_(pi/2)^pisqrt(x)sinxdx ~~ pi/16 { 1.25331 + 6.02892} #
# :. int_(pi/2)^pisqrt(x)sinxdx ~~ pi/16 { 7.28223} #
# :. int_(pi/2)^pisqrt(x)sinxdx ~~ 1.42986 #
# :. int_(pi/2)^pisqrt(x)sinxdx ~~ 1.430 # (3dp)

Related questions
See all questions in Integration Using the Trapezoidal Rule
Impact of this question
1652 views around the world
You can reuse this answer
Creative Commons License