Question

How do you verify whether rolle's theorem can be applied to the function `f(x)=1/x^2` in [-1,1]?

Answer 1

`f(x)` does not satisfy the conditions of Rolle's Theorem on the interval `[-1,1]`, as `f(x)` is not continuous on the interval

Explanation:

Rolle's Theorem states that if a function, `f(x)` is continuous on the closed interval `[a,b]`, and is differentiable on the interval, and `f(a)=f(b)`, then there exists at least one number `c`, in the interval such that `f'(c)=0`.

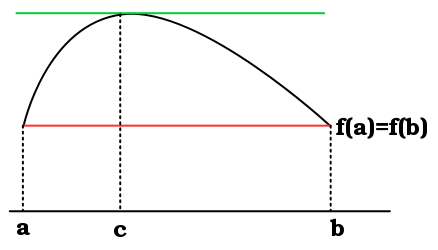
So what Rolle's Theorem is stating should be obvious as if the function is differentiable then it must be continuous (as differentiability `=>` continuity), and if its is continuous and `f(a)=f(b)` then the curve must chge direction (at least once) so it must have at least one minimum or maximum in the interval.

With `f(x)=1/x^2` with `x in [-1,1]`, then we can see `f(1)=1=f(-1)`, so our quest to verify Rolle's Theorem is to find a number `c` st `f'(c)=0`.

Differentiating wrt `x` we have, `f'(x)=-2x^-3=-(2)/x^3`

To find a turning point we require;

`f'(x)=0 => -(2)/x^3 = 0`

Which has no finite solution. We can conclude that `f(x)` does not satisfy the conditions of Rolle's Theorem on the interval `[-1,1]`, so it must be that `f(x)` is not continuous in that interval.

We can see that this is the case graphically, as f(x) has a discontinuity when `x=0 in [-1,1]`:

graph{1/x^2 [-10, 10, -2, 10]}