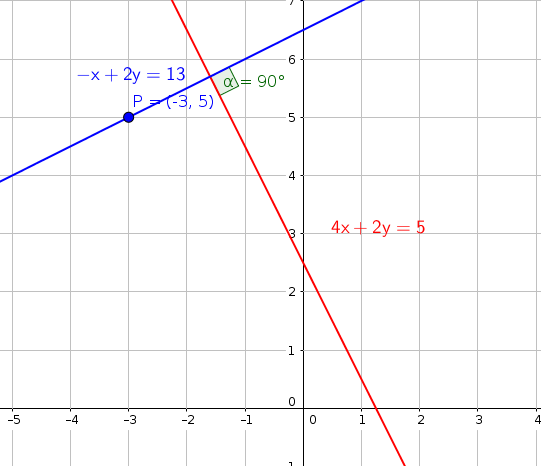
#4x+2y=5#
#"First,let us rearrange the equation above to find slope of the line."#
#color(red)(2y=-4x+5)#
#color(red)(y=-(4x)/2+5/2)#
#color(red)(y=-2x+5/2)#
#"in equation y=m x+n,the coefficient of the term x gives"#
#"the slope of the line."#
#"The slope of the red line is "m_r=-2.#
#"İf two line are perpendicular each other,the product of their "##"slopes is -1."#
#m_b*m_r=-1#
#m_b:"the slope of the blue line"#
#m_r:"the slope of the red line."#
#m_b*(-2)=-1#
#m_b=1/2#
#"Since the slope and one point is known,the equation of the blue"##"line can be written."#
#y-y_1=m(x-x_1#
#m=m_b=1/2#
#P(-3,5) " ; "x_1=-3" , "y_1=5#
#color(blue)(y-5=1/2(x+3))#
#color(blue)(y=1/2(x+3)+5)#
#color(blue)(y=1/2x+3/2+5)#
#color(blue)(y=1/2x+13/2)#
#"Or "#
#color(blue)(-x+2y=13)#

