How do you write an equation of a line that is parallel to #y+3x=7# and passes through point #(7,2)#?
1 Answer
I would use first your equation to find the SLOPE of your line. Basically the slope is a number that tells you what the inclination of your line is.
So, to find the parallel to your line you need a line with the same inclination...the same slope:
Your line:
Now the difficult bit...
The slope represents the inclination of your line and basically tells you how
For example, a big slope means that at every fixed change in
Have a look at this picture:
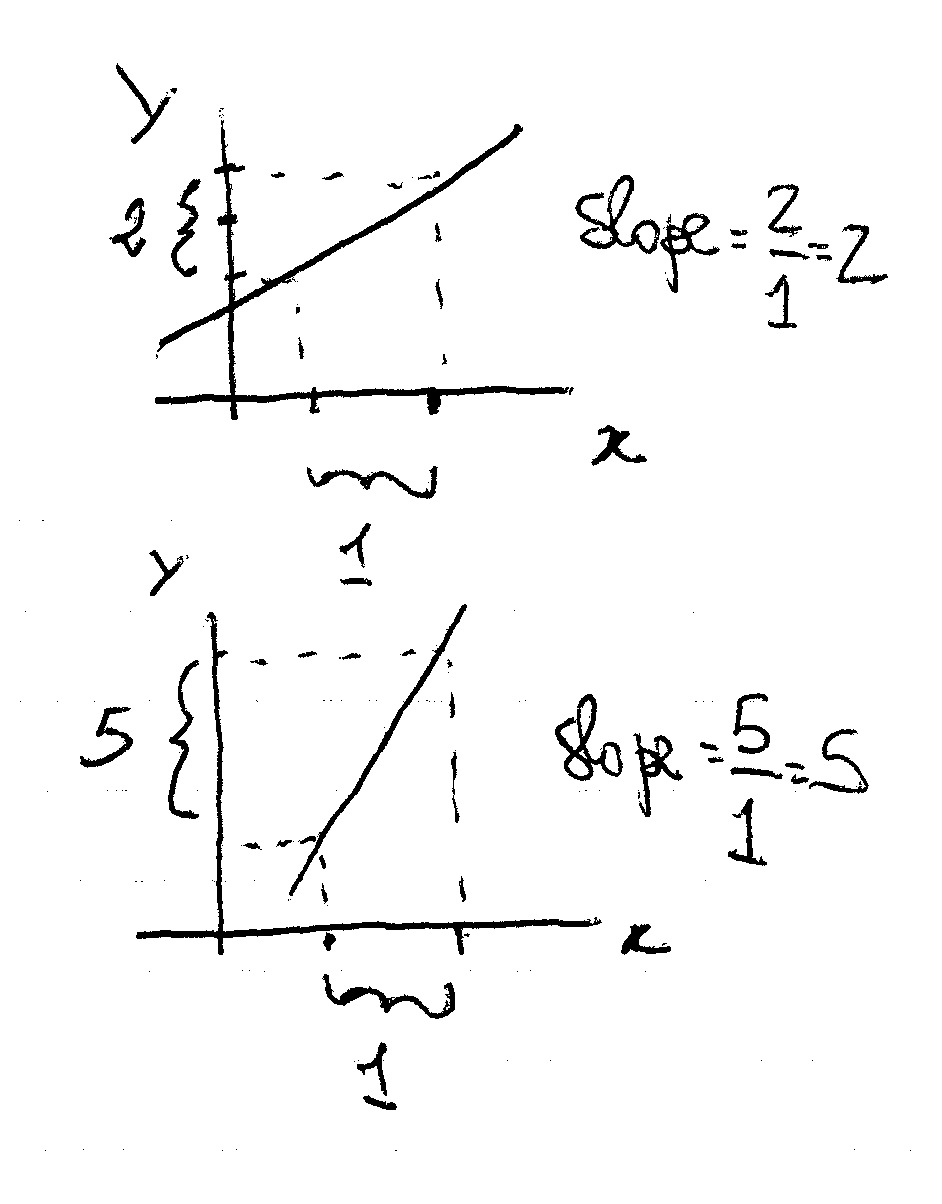
slope
To find your slope you simply take the change in
In your case:
Together with the coordinates of your point you can write:
Graphically:
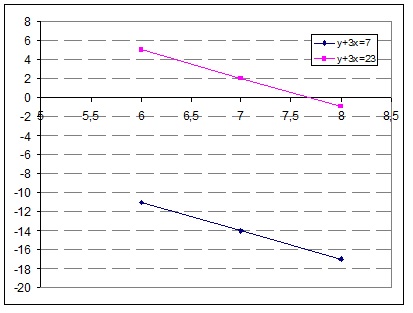
hope it helps

