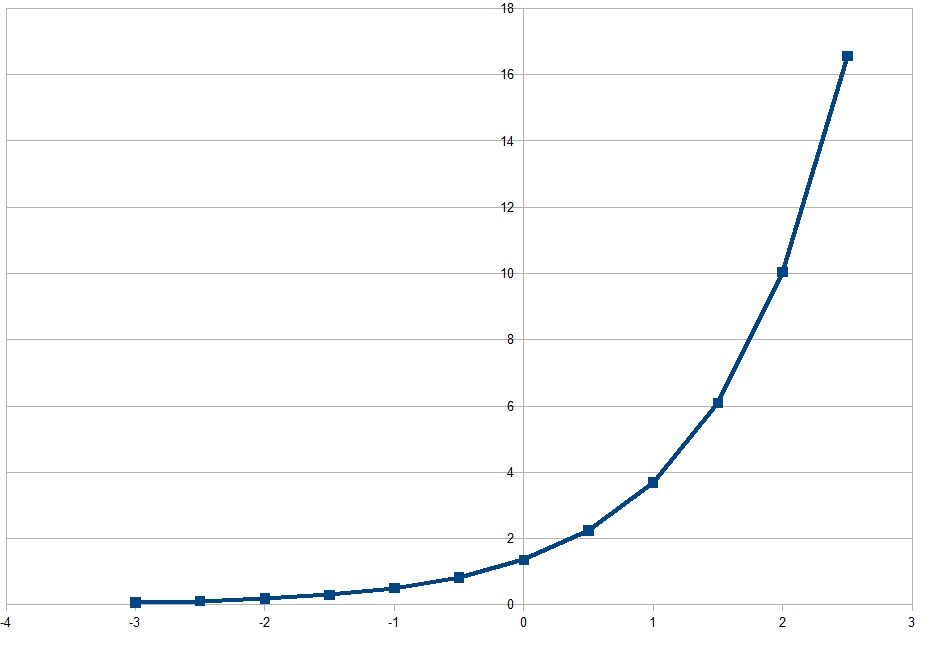
How do you write an exponential equation that passes through (-1, .5) and (2, 10)?
1 Answer
Aug 5, 2015
I found:
Explanation:
In general the equation will be of the form:
where:
let us use our points and substitute into our general equation:
from the first:
substitute into the second:
use the law of exponents and get:
take the
substitute back into
so finally your equation will be:
Graphically: