Question

How do you write the equation of the line that is perpendicular to the line `3x - 2y = 6` and passes through the point `(-1,2)`?

Answer 1

When given a line of the standard form:
`ax+by=c`
Swap "a" and "b":
`bx+ay=c`
Then change the sign of "a" or "b":
`-bx+ay=c` or `bx-ay=c`
Find a new value for "c" by substituting in the given point.

Explanation:

Given:

`3x - 2y = 6`

Swap "a" and "b":

`-2x + 3y = 6`

We shall change the sign of -2:

`2x + 3y = 6`

Determine a new value for c by substituting in the point, `(-1,2)`:

`2(-1)+3(2) = 4`

The equation of the desired line is:

`2x + 3y = 4`

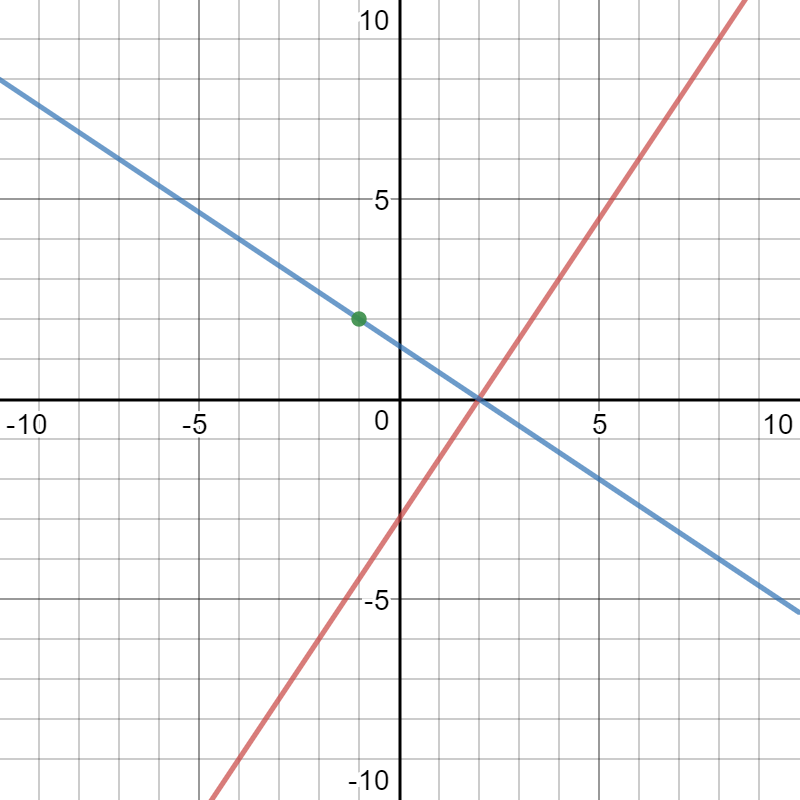
Here is a graph of the two lines and the point: