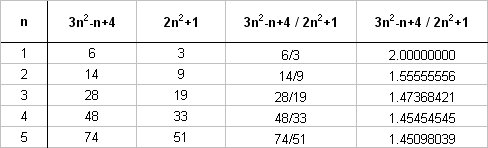
How do you write the first five terms of the sequence #a_n=(3n^2-n+4)/(2n^2+1)#?

Question

3313 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-06T20:22:39

# { 2, 14/9, 28/19, 48/33, 74/51 } #

We have:

# a_n=(3n^2-n+4)/(2n^2+1) #

Assuming that the first term is #n=1# as opposed to #n=0# then we simply evaluate the expression with #n=1#, as follows:

Put #n=1# then:

# a_1 = (3(1)^2-1+4)/(2(1)^2+1) #
# \ \ \ \ = (3-1+4)/(2+1) #
# \ \ \ \ = 6/3 #
# \ \ \ \ = 2 #

Similarly Put #n=2# then:

# a_2 = (3(2)^2-2+4)/(2(2)^2+1) #
# \ \ \ \ = (3.4-2+4)/(2.4+1) #
# \ \ \ \ = 14/9 #

etc.

The remaining terms have been calculated using excel: