How do you write the general form of a circle given center is (4,-6) and tangent to line x=-1?
1 Answer
Jan 15, 2016
Explanation:
The general form of a circle is
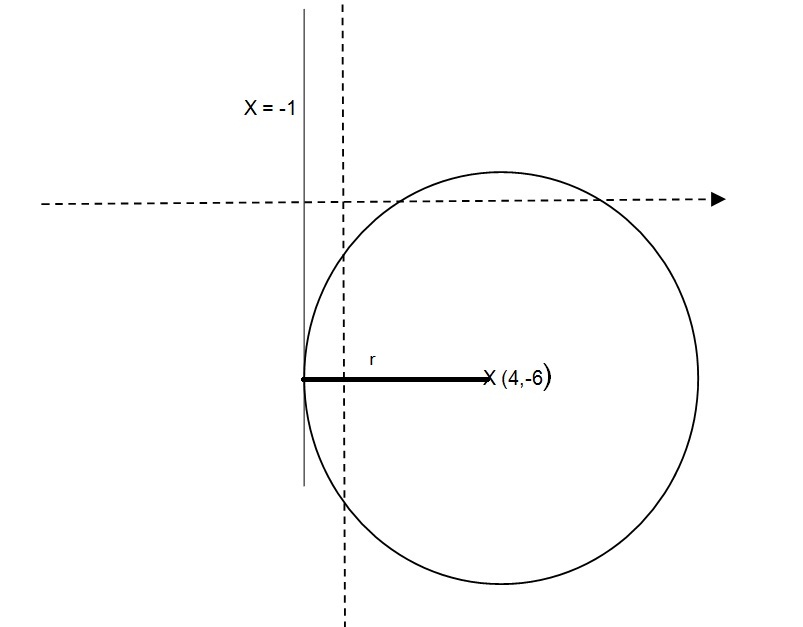
the radius can be calculated as the distance from the center to the tangent line, which is given by the difference in their x-coordinates.
The general equation is therefore

