How do you write the partial fraction decomposition of the rational expression #z/(z^4-1) #?
2 Answers
Dec 13, 2015
Answer is given as follows:
Explanation:
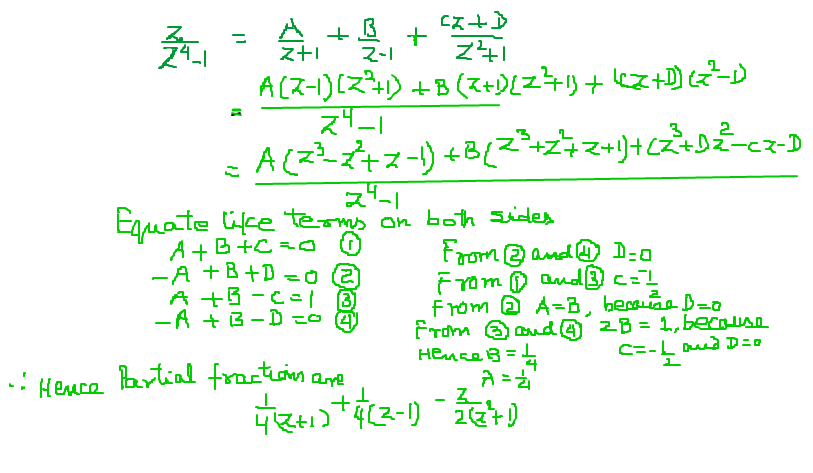
Dec 13, 2015
Explanation:
The expression equals
IF
IF
Plug in two values for
IF
IF
Solve the system to find that
Thus:

