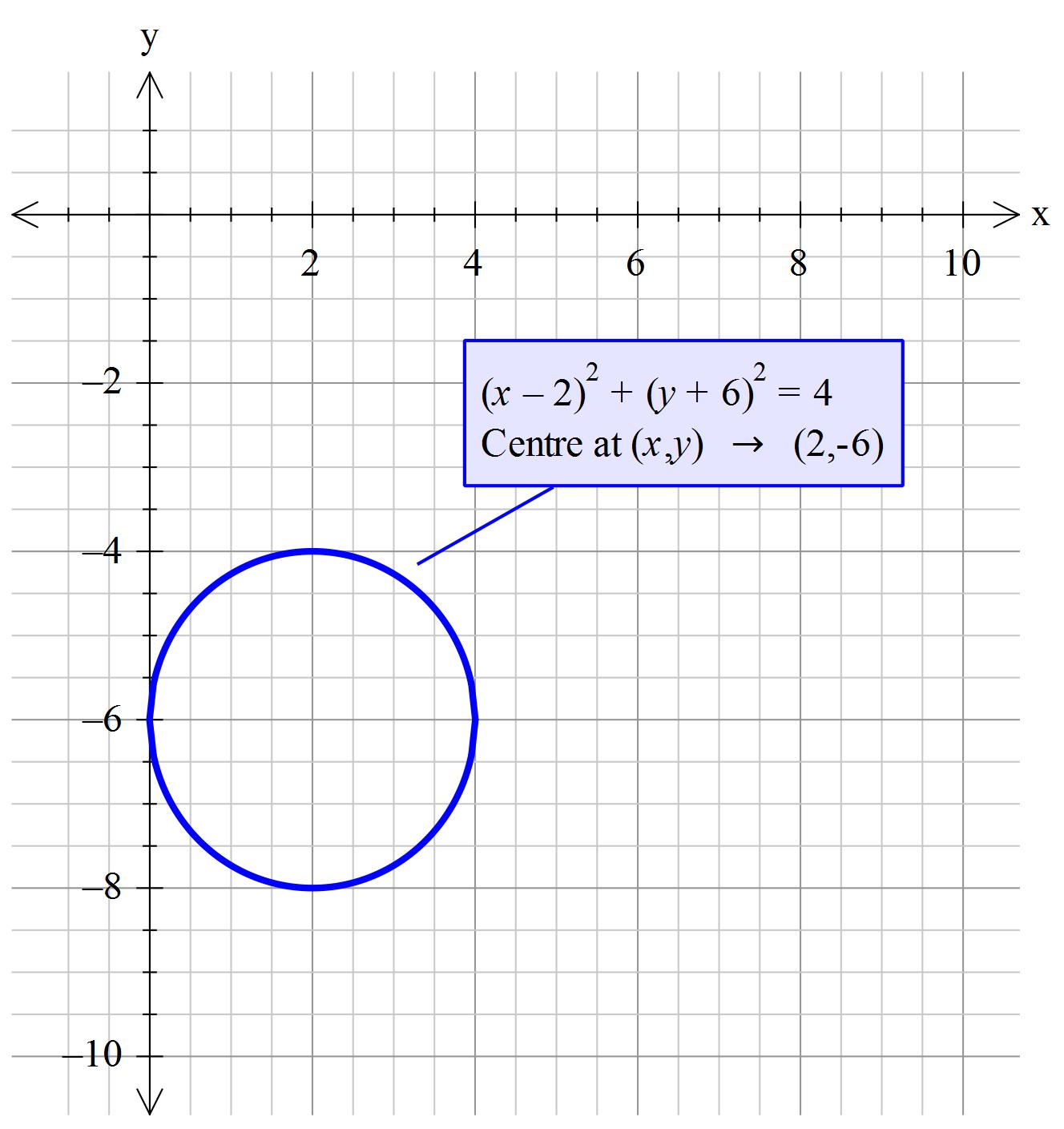
How do you write the standard from of the equation of the circle given center:(2,-6) radius: 2?

Question

1146 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-06-03T10:27:11

#color(green)((x-2)^2+(y+6)^2=2^2)#

See explanation as to why it is in this form.

The standardised formula for a circle with its centre at the origin is:

#x^2+y^2=r^2#

This is derived from Pythagoras rule about a 'right triangle'. You know the one; #a^2+b^2=c^2#

However, in this case the centre is not at the origin. It is at

#(x,y)->(2,-6)#

Consequently we mathematically move all the points as if the centre of the circle was at the origin so that #(x,y)->(0,0)#

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(brown)("Moving the "x's)#
#x_("moved")=x_("given")-2#

so each generic point we have #x-2#

#color(brown)("Moving the "y's)#
#y_("moved")=y_("given")+6#

so each generic point we have #y+6#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

#color(grown)(=>(x_("generic"))^2+(y_("generic"))^2 = r^2)#

Becomes:

#color(green)((x-2)^2+(y+6)^2=2^2)#

Tony B